Сегодняшнее занятие мы посвятим изучению следующего вида теплопередачи – конвекции. На прошлом занятии мы уже говорили о явлении теплопроводности, которое было связанно с тепловым движением частиц, в случае же конвекции речь будет идти не о движении отдельных частиц, а об их группах. Попробуем рассмотреть явление конвекции с позиции сравнения с явлением теплопроводности и выделения отличий между этими видами теплопередачи. Для этого проведем простой опыт.Опыт 1.С нагреванием льда в пробирке с водой. Наберем в пробирку воду, поместим на дно кусочек льда и начнем нагревать зажженной свечей у верхнего края, как это изображено на рисунке 1. Рис. 1. Нагревание льда в пробирке с водой. В ходе проведения опыта мы заметим, что верхняя часть пробирки очень нагреется и вода в этой части может даже закипеть, но лед при этом останется в своем кристаллическом состоянии и не растает. Если же теперь провести аналогичный опыт, но только расположить пламя свечи у нижнего края пробирки, то мы увидим, как весь лед быстро растает и вся вода со временем равномерно прогреется и даже, возможно, закипит. Проведенные опыты говорят о том, что в данном случае перенос энергии осуществляется не путем теплопроводности, а на основании некого другого явления, которое и имеет название конвекция. В переводе с латинского слово «конвекция» означает перенесение, перенос. Продемонстрируем опыты конвекции в газах и жидкостях на двух опытах. Опыт 3.Демонстрация явления конвекции в жидкости (воде). Опустим в правое и левое колено U-образной трубки с водой по ложке с марганцовкой, которая будет выступать в роли красителя для демонстрации конвективных потоков. Демонстрация конвекции в жидкости с помощью окрашивания конвективных потоков.Мы можем наблюдать явление, аналогичное предыдущему опыту: нагретая в пламени свечи вода расширяется, уменьшается ее плотность, и окрашенные марганцем потоки начнут подниматься вверх. Можно заметить, что со временем прогревания воды процесс конвекции протекает все интенсивнее, и конвективные потоки, доходя до верхней части трубки, начинают двигаться по горизонтальному участку трубки и опускаться в правом ее колене. Это происходит из-за того, что холодная вода в правом колене опускается вниз и движется по нижнему горизонтальному участку трубки, занимая место поднявшейся теплой воды. На основании проведенных опытов сделаем вывод о том, что такое явление конвекции. Конвекция – это явление переноса энергии струями, большими группами частиц жидкостей или газов. Т. е. по сравнению с явлением теплопроводности, когда при прогревании жидкостей или газов процесс передачи энергии частиц через их движение не так эффективен, как передача энергии путем движения целых групп частиц, вступает в действие более интенсивное способ теплопередачи путем конвекции. В результате рассмотренных свойств конвекции можно заметить, что она имеет место только в том случае, если речь идет о теплопередаче в веществе (а именно в жидкости или газе), если же вещества нет, то и не имеет смысла говорить о явлении конвекции. Различают два типа конвекции.
Вопросы: 1. Объясните, как и почему происходит перемещение воздуха над нагретой лампой. 2. Объясните, как происходит нагревание воды в колбе, поставленной на огонь. 3. В чем состоит явление конвекции? 4. Чем отличается естественная конвекция от вынужденной? 5. Почему жидкости и газы нагревают снизу? 6. Почему конвекция невозможна в твердых телах? Ответы: 1. Над нагретой лампой появляется горячий воздух который замещает холодный снизу происходит циркуляция воздуха. http://znanija.com/task/9350024 |
Введение в моделирование свободной конвекции в COMSOL Multiphysics®
Свободная конвекция играет важную роль во многих научных и прикладных задачах, таких как охлаждение электронных компонентов, кондиционирование в помещений и перенос вещества в окружающей среде. Модули Вычислительная гидродинамика и Теплопередача в версии 5.2a программного пакета COMSOL Multiphysics® включают функциональные возможности, позволяющие проще формулировать и решать задачи свободной конвекции. В этой статье мы расскажем о свободной конвекции, о новых функциональных возможностях и о некоторых проблемах, с которыми вы можете столкнуться при ее моделировании.
В этой статье мы расскажем о свободной конвекции, о новых функциональных возможностях и о некоторых проблемах, с которыми вы можете столкнуться при ее моделировании.
Что такое свободная конвекция?
Свободная конвекция — вид переноса вещества, вызванный действием выталкивающей (архимедовой) силы. Архимедова сила, в свою очередь, создается за счет неоднородной плотности среды переменного состава или температуры.
Вы могли сталкиваться с явлением свободной конвекции в системах кондиционирования помещений. В этом случае теплый воздух вблизи источников тепла поднимается вверх к потолку, а холодный воздух вблизи холодных поверхностей (таких как окна в зимний период) опускается вниз к полу.
Другой пример процесса, ход которого зависит от свободной конвекции, — охлаждение электроники. Например, нежелательно использовать шумные вентиляторы для охлаждения усилителей и телевизоров в домашних кинотеатрах. Электронное оборудование, работающее в тихой обстановке, обычно охлаждают с помощью свободной конвекции воздуха, обдувающего встроенные радиаторы.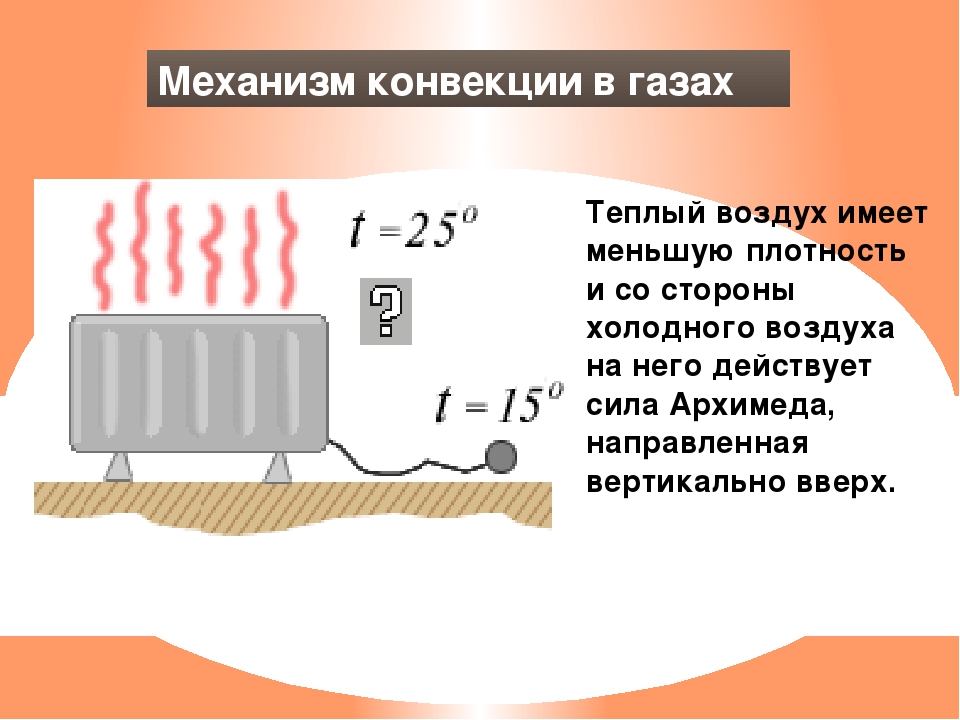
Свободная конвекция вокруг расходящегося игольчатого радиатора, нагреваемого снизу Анимация показывает величину скорости потока воздуха вокруг радиатора.
В химической и пищевой промышленности существуют менее очевидные задачи, связанные со свободной конвекцией. Экологи и метеорологи тоже сталкиваются с задачей свободной конвекции, когда пытаются предсказать и понять явления переноса в воздухе и в воде.
Во всех упомянутых случаях инженерам и ученым важно понимать свойства свободной конвекции и проектировать системы, позволяющие применять эти свойства. Математическое моделирование здесь незаменимо. В последней версии COMSOL Multiphysics определять и решать задачи, связанные со свободной конвекцией, стало еще проще. Для этого мы добавили ряд новых возможностей.
Вариант Weakly compressible flow (Слабосжимаемый поток) для гидродинамических интерфейсов не учитывает влияние волн давления, которые редко играют роль в процессах свободной конвекции. Это позволяет увеличить шаг по времени и сократить время вычисления для задач свободной конвекции.
Это позволяет увеличить шаг по времени и сократить время вычисления для задач свободной конвекции.
Вариант Incompressible flow (Несжимаемый поток) и приближение Буссинеска для потока, создаваемого архимедовой силой, линеаризуют плотность при помощи коэффициента термического расширения. Этот вариант учитывает изменение плотности в уравнении сохранения импульса только в слагаемом для объемной силы. Это еще более грубое упрощение по сравнению с вариантом
Функциональная возможность Gravity (Сила тяжести) позволяет легко задавать точку отсчета гидростатического давления и автоматически учитывает изменения гидростатического давления на вертикальных границах.
Давайте подробнее изучим эти новые возможности и научимся применять их к задачам моделирования свободной конвекции.
Как решать задачи свободной конвекции с помощью модели слабосжимаемой среды
Интерфейс Nonisothermal Flow (Неизотермический поток) предоставляет опцию Weakly Compressible Flow (Слабосжимаемый поток), которая упрощает решение задач конвекции, не учитывая изменения плотности из-за давления. Этот вариант также не учитывает волны давления, расчет которых требует плотную сетку и маленький временной шаг, а значит занимает много времени. Волны давления редко влияют на свободную конвекцию, поэтому мы мало потеряем в точности модели, применив такое упрощение.
Уравнение непрерывности для сжимаемой жидкости имеет вид
(1)
\[\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {\mathbf{u}}} \right) = 0\]
где ρ — плотность, а u — вектор скорости.
Для газа плотность пропорциональна давлению и температуре. Например, для идеального газа
(2)
\[\frac{{\partial \rho }}{{\partial t}} = \frac{{\partial p}}{{\partial t}}\frac{M}{{RT}} – \frac{{\partial T}}{{\partial t}}\frac{{pM}}{{R{T^2}}}\]
Если пренебречь динамическими эффектами изменения плотности, получим
(3)
\[\frac{{\partial \rho }}{{\partial t}} = – \frac{{\partial T}}{{\partial t}}\frac{{pM}}{{R{T^2}}}\]
Используя выражение для плотности идеального газа и пренебрегая зависимостью плотности от давления, получаем уравнение неразрывности
(4)
\[\frac{{\partial T}}{{\partial t}} + \nabla T \cdot {\mathbf{u}} – T\nabla \cdot {\mathbf{u}} = 0\]
Это означает, что изменение плотности обусловлено только изменением температуры. Изменение плотности может вызвать расширение текучей среды, но прямое динамическое влияние этого расширения на поле давления с настройками Weakly compressible flow (Слабосжимаемый поток) не учитывается.
Изменение плотности может вызвать расширение текучей среды, но прямое динамическое влияние этого расширения на поле давления с настройками Weakly compressible flow (Слабосжимаемый поток) не учитывается.
Кроме выражения для плотности в уравнении неразрывности, можно добавить объемную силу, сонаправленную силе тяжести, к уравнению сохранения импульса, выбрав флажок Gravity (Сила тяжести) в настройках интерфейса потока среды. По умолчанию она направлена в отрицательном направлении оси z. Эта сила имеет вид
(5)
\[{F_z} = -g\rho \left( T \right)\]
где плотность ρ зависит от температуры.
Для идеального газа плотность обратно пропорциональна температуре.
Вы можете найти настройки для варианта Weakly compressible flow (Слабосжимаемый поток), выбрав интерфейс Nonisothermal Flow (Неизотермический поток) или интерфейс Conjugate Heat Transfer (Сопряженная теплопередача). Выберите в Построителе моделей интерфейс Fluid Flow (Поток текучей среды), чтобы увидеть окно настроек, как на рисунке ниже. Выбрав вариант Weakly compressible flow (Слабосжимаемый поток), вы устраните зависимость между давлением и плотностью, а включив флажок Gravity (Сила тяжести) — автоматически добавите объемную силу к уравнению импульса.
Выбрав вариант Weakly compressible flow (Слабосжимаемый поток), вы устраните зависимость между давлением и плотностью, а включив флажок Gravity (Сила тяжести) — автоматически добавите объемную силу к уравнению импульса.
Окно настроек интерфейса Fluid Flow (Поток текучей среды), показывающее опции Weakly compressible flow (Слабосжимаемый поток) и Gravity (Сила тяжести).
На графике ниже показан поток между двумя вертикальными печатными платами. На рисунке показана только элементарная ячейка одной печатной платы. Вторая печатная плата размещена непосредственно перед ней, задней стороной к той плате, которую мы видим. Поток полностью обусловлен архимедовой силой, вентилятора нет.
Скорость потока на входе составляет примерно 0,2 м/с, а на выходе — примерно 0,3 м/с. Воздух не поступает с боковых сторон, а значит, разность скоростей потока обусловлена расширением воздуха из-за повышения температуры воздуха в канале между двумя печатными платами.
Созданный архимедовой силой поток между двумя вертикальными печатными платами. Расширение показано с помощью цветовой схемы стрелок: скорость потока на входе примерно 0,2 м/с, а на выходе — примерно 0,3 м/с.
Несжимаемая среда с приближением Буссинеска
Если изменения плотности и связанное с ними расширение пренебрежимо мало влияют на поле скорости потока, мы можем использовать опцию Incompressible flow (Несжимаемый поток) и приближение Буссинеска для свободной конвекции. Тогда уравнение неразрывности еще больше упрощается, чем в случае опции Weakly compressible flow (Слабосжимаемый поток), потому что текучая среда теперь считается несжимаемой. Уравнение неразрывности принимает вид
(6)
\[\nabla \cdot {\mathbf{u}} = 0\]
Вместо этого малые изменения плотности учитываются посредством объемной силы, которую добавляют в уравнение сохранения импульса и которая направлена противоположно силе тяжести, то есть, по умолчанию, в направлении оси z. Малые изменения плотности вычисляют, линеаризуя температурную зависимость плотности среды. Z-компонента объемной силы становится равна
Малые изменения плотности вычисляют, линеаризуя температурную зависимость плотности среды. Z-компонента объемной силы становится равна
(7)
\[{F_z} = g{\rho _{{\text{ref}}}}\alpha \Delta T\]
где g — постоянная силы тяжести, \[{\rho _{{\text{ref}}}}\] — плотность при исходной температуре, α — коэффициент термического расширения среды, ΔT — разность температур.
Преимущество приближения Буссинеска для потоков, создаваемых архимедовой силой, заключается в уменьшении нелинейной составляющей уравнений гидродинамики — такую задачу проще решить численно, она требует меньше итераций и позволяет использовать большие шаги по времени в нестационарных задачах.
Например, приближение Буссинеска дает близкое к реальности описание потока воды при относительно малых разностях температуры. На рисунке ниже показана свободная конвекция в стакане воды, который нагревают снизу. Мы наблюдаем очень сложную картину потоков: потоки в центре и у дна стакана направлены вверх, а потоки между стенками и центром стакана направлены вниз.
Свободная конвекция в стакане воды. График показывает поле скорости потока в стакане и распределение температуры на стенках стакана.
Мы можем использовать вариант Incompressible flow (Несжимаемый поток) вместе с приближением Буссинеска для потока, обусловленного архимедовой силой, выбрав настройки для гидродинамических интерфейсов в COMSOL Multiphysics, показанные на рисунке ниже.
Опции Incompressible flow (Несжимаемый поток), Gravity (Сила тяжести) и упрощенное задание давления позволяют использовать приближение Буссинеска для задачи свободной конвекции.
Задание уравнения для давления в моделях свободной конвекции
При моделировании сжимаемого потока зависимость давления от времени включена в уравнение непрерывности, поскольку для сжимаемых текучих сред плотность является функцией давления. Это означает, что для хорошей постановки задачи обычно достаточно задать начальное условие по давлению, даже если мы не задаем давление на границе.
Для слабосжимаемых и несжимаемых потоков, как мы обсуждали выше, зависимость давления от времени в уравнении непрерывности опускается. Если граничные условия не задают давление, то поле давления не может быть однозначно определено до тех пор, пока мы не зададим давление хотя бы в одной точке области.
В COMSOL Multiphysics мы можем задать так называемое ограничение давления в точке, чтобы избежать неопределенности при расчете поля давления. Отсутствие условия для точки отсчета давления часто приводит к проблемам со сходимостью в задачах свободной конвекции.
Настройки для ограничения давления в точке на примере со стаканом воды.
Использование связывания и разделения переменных для задач свободной конвекции
Уравнения, описывающие свободную конвекцию, обычно включают уравнение сохранения импульса, уравнение неразрывности и уравнение переноса энергии или массообмена. Если выталкивающая сила создается разностью температур, то уравнение энергетического обмена жестко связано с уравнениями гидродинамики (уравнения Навье–Стокса).
Узел Solver (Решатель) в дереве модели и настройки полностью связного решателя.
Для очень больших задач предпочтительным может оказаться раздельный подход. Например, если в задаче есть несколько химических веществ и выталкивающая сила создается за счет разного химического состава, то решатель с разделением переменных может оказаться единственным вариантом, не требующим чрезмерного объема памяти.
Заключение
Я хотел бы закончить эту статью еще одним примером, связанным со свободной конвекцией. Я часто думаю о свободной конвекции, куря сигару. Хотя я и не хочу рекламировать сигары, мой любимый пример свободной конвекции — сигарный дым, поднимающийся в холодный зимний воздух. На рисунке ниже показана зажженная сигара на пепельнице и распределение скорости в потоке, вызванном теплом сгорания.
Свободная конвекция (с небольшой составляющей вынужденной конвекции) воздуха вокруг зажженной сигары на пепельнице.
Часть потока вокруг зажженной сигары на самом деле создается вынужденной конвекцией, так как большая часть табака превращается в дым и плотность меняется с 500–1000 кг/м
Дополнительная литература
- Прочитайте другие статьи о свободной конвекции и моделировании гидродинамики в блоге COMSOL:
Конвекция свободная, вынужденная — Энциклопедия по машиностроению XXL
Конвекция свободная, вынужденная 14 [c.230]Вынужденной конвекцией называется движение жидкости, вызванное действием внешних поверхностных сил, создаваемых работой насосов, компрессоров и т. д. В отличие от свободной вынужденная конвекция может и не сопровождаться теплообменом (изотермическое течение) в этом случае осуществляется конвективный перенос массы.
Интенсивность теплоотдачи зависит от многих факторов и в частности от вида конвекции (свободная или вынужденная), режима течения жидкости (ламинарный или турбулентный), физических свойств среды (плотности р, теплопроводности X, динамической вязкости (Г, массовой удельной теплоемкости с, коэффициента объемного расширения
То /(уа) свободной конвекции на вынужденное течение несущественно. [c.104]
В этом параграфе будет рассмотрено свободное гравитационное течение для наиболее простых форм поверхности твердого тела (вертикальная плита, горизонтальный цилиндр) Предполагается, что объем жидкости настолько велик, что свободное движение, возникающее у других тел, расположенных в этом объеме, не сказывается на рассматриваемом течении. Как и при вынужденной конвекции, свободное движение жидкости может быть как ламинарным, так и турбулентным.
Как и при вынужденной конвекции, свободное движение жидкости может быть как ламинарным, так и турбулентным.
Условия подобия процессов конвективного теплообмена при совместном свободно-вынужденном движении теплоносителя. Анализ условий подобия раздельно для случаев вынужденного движения и свободной конвекции был проведен выше. На практике, однако, встречаются также случаи, когда одновременно с вынужденным движением в системе под действием подъемных сил развиваются токи свободной конвекции, т. е. имеет место свободно-вынужденное течение теплоносителя. В таком более сложном случае для выполнения условий подобия процессов необходима инвариантность (одинаковость) уже не двух, а трех определяющих чисел подобия Рейнольдса Re, Грасгофа Gr и Прандтля Рг. Соответствующее уравнение подобия для теплоотдачи при совместном свободно-вынужденном движении принимает вид
Физические свойства жидкости, входящие в числа Ре и Nu, а также выбираются при температуре, равной полусумме температур стенки и средней по длине трубы температуры жидкости Что касается оговорки по поводу отсутствия влияния силы тяжести (свободной конвекции) на вынужденное течение, то ее можно
[c. 128]
128]
Для начала кипения необходимо несколько перегреть теплоноситель относительно температуры насыщения. Этот перегрев определяется давлением, температурой недогрева теплоносителя, скоростью среды, материалом и характером поверхности, смачиваемостью и т. п. Кипение принято подразделять на пузырьковое и пленочное. Процессы кипения подразделяют также по типу конвекции и выделяют кипение при свободной, вынужденной, смешанной конвекции. Термины развитое и неразвитое относят к процессам пузырькового кипения. Когда пузырьковое кипение и чистая конвекция попеременно сменяют друг друга, процесс теплообмена становится неустойчивым. [c.139]
Разница в результатах расчета критической тепловой нагрузки по формуле(9) для случаев свободной конвекции и вынужденного движе- [c.73]
Исследование влияния вибрации и вращения поверхности нагрева. Выше было показано влияние искусственной турбулизации потока на интенсивность конвективного теплообмена. Создание закрученного потока повышает скорость движения потока жидкости, что приводит к увеличению интенсивности теплоотдачи. Такого же увеличения скорости можно достигнуть не за счет движения среды, а за счет движения поверхности теплообмена. Так, при вращении цилиндра в неограниченном объеме частицы жидкости вследствие вязкости вовлекаются в круговое движение. Частицы жидкости, находящиеся на поверхности, движутся с такой же скоростью, с какой вращается контур цилиндра по мере удаления от поверхности скорость движения жидкости уменьшается, а вдали от нее практически отсутствует. Вращение цилиндров производится электромотором через шкив или мотор постоянного тока, позволяющие изменять скорость вращения. Вращение цилиндра приводит к значительному увеличению скорости обтекания цилиндра, а следовательно, его теплоотдачи. При этом увеличение скорости не сопровождается повышением гидравлического сопротивления, определяемого формой тела. Опытное исследование теплоотдачи одиночных цилиндров при их вращении и вибрации проводилось в ряде работ Л.
Создание закрученного потока повышает скорость движения потока жидкости, что приводит к увеличению интенсивности теплоотдачи. Такого же увеличения скорости можно достигнуть не за счет движения среды, а за счет движения поверхности теплообмена. Так, при вращении цилиндра в неограниченном объеме частицы жидкости вследствие вязкости вовлекаются в круговое движение. Частицы жидкости, находящиеся на поверхности, движутся с такой же скоростью, с какой вращается контур цилиндра по мере удаления от поверхности скорость движения жидкости уменьшается, а вдали от нее практически отсутствует. Вращение цилиндров производится электромотором через шкив или мотор постоянного тока, позволяющие изменять скорость вращения. Вращение цилиндра приводит к значительному увеличению скорости обтекания цилиндра, а следовательно, его теплоотдачи. При этом увеличение скорости не сопровождается повышением гидравлического сопротивления, определяемого формой тела. Опытное исследование теплоотдачи одиночных цилиндров при их вращении и вибрации проводилось в ряде работ Л. 3, 4] в условях свободной, вынужденной, а также при одновременном действии обоих видов конвекции. Общий эффект теплоотдачи определяется всеми указанными факторами. При обработке опытных данных имеется возможность сохранить вид прежних расчетных уравнений и с учетом интенсификации конвективного теплообмена дополнительной скоростью.
[c.223]
3, 4] в условях свободной, вынужденной, а также при одновременном действии обоих видов конвекции. Общий эффект теплоотдачи определяется всеми указанными факторами. При обработке опытных данных имеется возможность сохранить вид прежних расчетных уравнений и с учетом интенсификации конвективного теплообмена дополнительной скоростью.
[c.223]
При таком физическом обосновании постановки задачи ее решение приобретает определенную направленность и однозначность. Построение расчетных формул по сложному переносу резко упрощается, если рассматривать две зоны одну зону с превалирующим влиянием инерционной силы, где гравитационная сила является сопутствующей, и другую, в которой превалирующее значение имеет свободная конвекция, а вынужденная является сопутствующей. [c.283]
Температурные поля в движущейся среде существенным образом зависят от полей скорости. С другой стороны, те.мпературное поле вызывает нарушение плотности среды, в результате чего возникает конвективное движение частиц, называемое свободной конвекцией. Наряду со свободной конвекцией различают вынужденную конвекцию, когда движение среды обусловливается внешним механическим или другим воздействием (нагнетающее или всасывающее действие насосов, компрессоров, вентиляторов и пр.). В общем случае наряду с вынужденной одновременно может быть и свободная конвекция. Относительное влияние последней на теплообмен тем больше, чем больше разность температур отдельных частиц жидкости и чем меньше скорость вынужденного движения.
[c.161]
Наряду со свободной конвекцией различают вынужденную конвекцию, когда движение среды обусловливается внешним механическим или другим воздействием (нагнетающее или всасывающее действие насосов, компрессоров, вентиляторов и пр.). В общем случае наряду с вынужденной одновременно может быть и свободная конвекция. Относительное влияние последней на теплообмен тем больше, чем больше разность температур отдельных частиц жидкости и чем меньше скорость вынужденного движения.
[c.161]
Влияние свободной конвекции на вынужденное течение отражает число Ог (или Ог Рг). Бели оно мало, то течение будет вязкостным или вязкостно-инерционным. При достаточно больших значениях числа Ог наблюдается переход к вязкостно-гравитационному или вязкостно-инер-ционно-гравитационному течению. [c.47]
Заметим в заключение, что уравнения (7-83) и (7-84) относятся к случаю вязкостного течения жидкости, когда влияние свободной конвекции на вынужденное течение, а следовательно, и на теплоотдачу несущественно. Это условие приближенно выполняется, если [Ог-Рг[c.142]
Это условие приближенно выполняется, если [Ог-Рг[c.142]
В случае наложения свободной конвекции на вынужденное течение градиент скорости на стенке будет зависеть от параметров, определяющих не только вынужденное, но и свободное течение. В этом случае величина А заранее неизвестна, однако она может быть определена из уравнения движения. Воспользуемся уравнением движения в упрощенной форме, опуская инерционные члены, но учитывая подъемную силу. Полагая физические свойства жидкости (кроме плотности) постоянными и представив плотность в виде линейной функции температуры получим [c.320]
Вынужденной конвекцией называется движение жидкости, вызванное действием внешних поверхностных сил, создаваемых работой насосов, компрессоров и т. д. В отличие от свободной вынужденная конвекция может и не сопровождаться теплообменом (изотермическое течение) в этом случае осуществляется конвективный перенос массы. Вынужденная конвекция в общем случае может сопровож- [c.
 156]
156]Конвекции при вынужденном движении противопоставляется конвекция при свободном движении, когда сила тяжести оказывается главной активной силой, возбуждающей течение среды в границах изучаемого поля. Конечно, могут иметь место и смешанные случаи, при которых эффекты свободного и вынужденного движения соизмеримы друг с другом, однако почти невероятно, чтобы одновременно следовало бы учитывать влияние числа М. [c.76]
Свободная конвекция воды 10 l(i Вынужденная конвекция la- [c.89]
Режим движения вязкостно-гравитационный, и для случая совпадения вынужденной и свободной конвекций у стенки расчет теплоотдачи проводим по формуле (5-5) [c.82]
Одновременный перенос теплоты конвекцией и теплопроводностью называют конвективным теплообменом-, он может быть свободным и вынужденным. Если движение рабочего тела вызвано искусственно (вентилятором, компрессором, мешалкой и др.), то такой конвективный теплообмен называют вынужденным. Если же движение рабочего тела возникает под влиянием разности плотностей отдельных частей жидкости от нагревания, то такой теплообмен называют свободным, или естественным, конвективным теплообменом.
[c.346]
Если же движение рабочего тела возникает под влиянием разности плотностей отдельных частей жидкости от нагревания, то такой теплообмен называют свободным, или естественным, конвективным теплообменом.
[c.346]
Различают конвекцию вынужденную (движение жидкости создается искусственно) и свободную — движение возникает в связи с ее нагреванием и изменением плотности. [c.402]
В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому критериальное уравнение теплоотдачи упрощается [c.423]
При свободном движении жидкости, когда вынужденная конвекция отсутствует, вместо критерия Рейнольдса в критериальное уравнение теплоотдачи необходимо ввести критерии Грасгофа. Отсюда получаем [c.424]
Как указывалось выше (п. 8.2.3), теплообмен при развитом пузырьковом кипении полностью управляется своими внутренними механизмами и не зависит от скорости вынужденного движения. Однако это не означает, что вынужденное движение вообще не влияет на закономерности кипения. Прежде всего с ростом скорости течения жидкости Wq возрастает коэффициент теплоотдачи однофазной конвекции и, следовательно, при неизменной плотности потока q уменьшается перегрев стенки относительно. Это приводит к тому, что начало кипения в потоке жидкости происходит при тем больших q, чем выше скорость жидкости. Эта закономерность хорошо видна из рис. 8.5, на котором представлены сглаженные опытные зависимости q(AT), полученные одним из авторов [17]. Теплообмен происходил на омываемой потоком воды плоской пластине при давлении 3,92 бар. Кривая 1 соответствует кипению при свободном движении (в большом объеме). В условиях обтекания пластины потоком воды до начала закипания коэффициент теплоотдачи не зависит от плотности теплового потока и целиком определяется скоростью жидкости (кривые 2, 3, 4). С ростом теплового потока при постоянном а, растет температура стенки, и при некотором значении
[c.
Однако это не означает, что вынужденное движение вообще не влияет на закономерности кипения. Прежде всего с ростом скорости течения жидкости Wq возрастает коэффициент теплоотдачи однофазной конвекции и, следовательно, при неизменной плотности потока q уменьшается перегрев стенки относительно. Это приводит к тому, что начало кипения в потоке жидкости происходит при тем больших q, чем выше скорость жидкости. Эта закономерность хорошо видна из рис. 8.5, на котором представлены сглаженные опытные зависимости q(AT), полученные одним из авторов [17]. Теплообмен происходил на омываемой потоком воды плоской пластине при давлении 3,92 бар. Кривая 1 соответствует кипению при свободном движении (в большом объеме). В условиях обтекания пластины потоком воды до начала закипания коэффициент теплоотдачи не зависит от плотности теплового потока и целиком определяется скоростью жидкости (кривые 2, 3, 4). С ростом теплового потока при постоянном а, растет температура стенки, и при некотором значении
[c. 355]
355]
В зависимости от причин возникновения конвективного движения жидкости или газа различают свободную и вынужденную конвекции. При свободной конвекции перемещение теплоносителя происходит только под влиянием разности плотностей холодной и горячей жидкости или газа в поле тяготения. Нагревшиеся объемы теплоносителя поднимаются вверх, охладившиеся опускаются. Около нагретых тел имеет место, как правило, восходящая (подъемная) конвекция, а у холодных — опускная (нисходящая). [c.89]
Как отмечалось выше, различают два вида конвекции вынужденную и свободную. [c.93]
Конвекция, как ранее сказано, бывает вынужденной и свободной. Вынужденное движение может сопровождаться свободным движением. При этом влияние свободного движения тем больше, чем меньше скорость вынужденного движения и больше разность температур отдельных частиц среды. При больших скоростях вынужденного движения свободную конвекцию можно не учитывать ввиду ее небольшого влияния. Процесс конвективного теплообмена, характеризуемый совокупиостью тепловых и гидромеханических явлений, может быть описан системой дифференциальных уравнений.
[c.309]
Процесс конвективного теплообмена, характеризуемый совокупиостью тепловых и гидромеханических явлений, может быть описан системой дифференциальных уравнений.
[c.309]
КРИТИЧЕСКИЕ ТЕПЛОВЫЕ НАГРУЗКИ ПРИ СВОБОДНОЙ КОНВЕКЦИИ И ВЫНУЖДЕННОМ ДВИЖЕНИИ КИПЯЩЕГО И НЕДОГРЕТОГО ДАУТЕРМА [c.56]
КОНВЕКЦИЯ (от лат. onve tio — доставка) — перенос массы в результате перемещения сплошной среды (газа, жидкости). Существуют различные виды К. в зависимости от причин, её порождающих наиболее распространённые — свободная, вынужденная и капиллярная К. [c.435]
Клячко Л. С., К вопросу о теплообмене между газом и шаровой поверхностью в условиях совместного действия свободной и вынужденной конвекций, Trans. ASME, s С. ( Теплопередача ), 1963, № 4. [c.407]
При неодинаковой температуре в сечении возникает естественная конвекция и создается подъемная сила. Это влияет па п[)офиль скорости, причем характер изменения профиля скорости зависит от того как расположена труба, вертикально или горизонтально, и совпадают ли направления свободного и вынужденного движений или они противоположны. Для вертикальной трубы в случае совпадения направлений свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее сверху или нагреве жидкости и подаче ее снизу) у стенки трубы скорость возрастает, а в центре уменьшается (рис. 1.7, а). В случае противоположно направленных свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее снизу или нагревании жидкости и подаче ее сверху) скорость у стенки трубы становится меньше, а в центре больше (рис. 1.7, 6).
[c.21]
Для вертикальной трубы в случае совпадения направлений свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее сверху или нагреве жидкости и подаче ее снизу) у стенки трубы скорость возрастает, а в центре уменьшается (рис. 1.7, а). В случае противоположно направленных свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее снизу или нагревании жидкости и подаче ее сверху) скорость у стенки трубы становится меньше, а в центре больше (рис. 1.7, 6).
[c.21]
В горизонтальной трубе вследствие свободного дпижсшня (конвекции) возникает поперечная циркуляция капельной жидкости (рис. 1.8). Частицы жидкости одновременно участвуют в поперечной циркуляции и в продольном вынужденном движении. В результате сложения этих движений траектории частиц приобретают сложный вид винтовых линий. [c.21]
Члены, стоящие в левой части уравнения энергии, называются конвективными и определяют вынужденную конвекцию. Может существовать также свободная конвекция, природа которой обусловлена Архимедовой подъемной силой, вызванной подогревом жидкости. Обозначим через р коэффициент объемного расширения среды через АТ повышение температуры данной частицы среды, по сравнению с ненагретыми частицами. Тогда р АТ есть относительное изменение объема данной частицы, а Архимедова подъемная сила будет равна Fa = pg P AT g— ускорение свободного падения). Полученную силу, отнесенную к единице массы, можно рассматривать как массовую силу и ввести ее в уравнение движения (1.18) в качестве/
[c.39]
Может существовать также свободная конвекция, природа которой обусловлена Архимедовой подъемной силой, вызванной подогревом жидкости. Обозначим через р коэффициент объемного расширения среды через АТ повышение температуры данной частицы среды, по сравнению с ненагретыми частицами. Тогда р АТ есть относительное изменение объема данной частицы, а Архимедова подъемная сила будет равна Fa = pg P AT g— ускорение свободного падения). Полученную силу, отнесенную к единице массы, можно рассматривать как массовую силу и ввести ее в уравнение движения (1.18) в качестве/
[c.39]
Различают свободную и вынужденную конвекцию. Конвекция, создаваемая принудительным способом (мешалкой, вентилятором и т д.), носит название вынужденной. Если же движение элементов объема среды вызвано наличием в ней температурных разностей, а следовательно, разных плотностей, то такая конвекция называется свободной или естественной. Она создается за счет того, что более холодные частицы жидкости или газа, имеющие большую плотность, под денстпнем гравитационного поля Земли опускаются вниз, а более нагретые под действием архимедовой силы иодип-маются вверх. [c.76]
[c.76]
Характер распределения Aopo Teii в пограничном с/.ое при свободной конвекции (см, сечение /—/ на рис. 17,9) отличается от такопого при вынужденной конвекции. При свободной конвекции скорость сначала возрастает от нуля у стеик1 до максимального значения, а затем вновь у.меньшается до и ля на границе пограничного слоя. [c.195]
Menumaster MRX523BL, профессиональная печь комбинированная СВЧ, конвекция
Menumaster MRX523BL, профессиональная печь комбинированная СВЧ, конвекция.
Высокоскоростная профессиональная комбинированная печь MRX51 идеально впишется в интерьер любого заведения: кинотеатры, рестораны, кофейни, АЗС и другие заведения общественного питания.
Эти компактные модели отличаются широким функционалом и обеспечивают непревзойденный результат готовки вне зависимости от приготавливаемого блюда.
Свойства модели:
- Компактная конструкция из качественной нержавеющей стали.

- Оборудована глухой дверцей с инновационной ручкой. Открытие дверцы — вниз.
- Внутренняя сторона двери и камера оклеены специальной защитной антипригарной плёнкой.
- Не требует установки вытяжного зонта.
- Многоуровневая структура меню.
- Обновление и программирование можно осуществлять через Wi Fi, USB-порт, Ethernet.
- Камера: 31,2 х 31,2 х 17,8 см.
- Объем камеры: 17,2 л.
- Вариация температур: 95 — 270°С.
- Тип конструкции: настольная.
- Самый большой в линейке цветной сенсорный дисплей.
- Сохранение и обновление программ через USB-порт, Ethernet, Wi Fi.
- Возможность программирования до 1200 программ готовки;.
- Легкий доступ к внутренним компонентам для обслуживания и чистки.
- Скорость вентилятора программируется.
- 3 воздушных съёмных фильтра с функцией напоминания об очистке.
- Русифицированное меню управления.
- Закрытые ТЭНы.
- USB, Wi-Fi, Ethernet.
- Лопатка в комплекте.

С турбопечью MRX523BL Вы всегда получаете прекрасный результат.
Мощный и эффективный способ,чтобы…
- Быстро подавать качественные блюда.
- Увеличить прибыль и продажи блюд.
- Готовить более свежую и горячую пищу по требованию.
Максимизируйте свою прибыль!
Мощная высокоскоростная печь MRX создана, чтобы справиться с быстрым темпом и высокими требованиями самых загруженных кухонь. Это высокопроизводительное устройство для работы в тяжелых условиях идеально подходит для широкого спектра применения в сфере общественного питания.
40 лет назад Litton Industries, один из лидеров и новаторов в области СВЧ-оборудования, представил бренд MENUMASTER. Около 20 лет назад компания Amana® приобрела бренд Menumaster.
В настоящее время Amana и Menumaster стали синонимами ― брендами, которые представляют решения по высокоскоростному приготовлению пищи. Бренд Menumaster обеспечен превосходным обслуживаем и всесторонней поддержкой (как сервисной, так и кулинарной). Долгая история развития, а также приоритет качества и надежности оборудования позволяет считать печи Menumaster лучшим помощником на профессиональной кухне.
Бренд Menumaster обеспечен превосходным обслуживаем и всесторонней поддержкой (как сервисной, так и кулинарной). Долгая история развития, а также приоритет качества и надежности оборудования позволяет считать печи Menumaster лучшим помощником на профессиональной кухне.
Amana® представляет линейку печей, которые смогут удовлетворить запросы любого предприятия питания: от моделей малой мощности до сверхмощных печей с двумя магнетронами, рассчитанных на высокие нагрузки в течение дня.
Компания Amana® с гордостью может сказать, что является единственным производителем СВЧ-печей, имеющим завод по сборке на территории США.
Печам Menumaster доверяют ведущие мировые ресторанные сети и сети фаст-фуда, так как они уверены в надежности и выносливости этих печей. Подтверждением высокого уровня продукции стала награда «Лучший в отрасли» в сегменте СВЧ-печей, которую компания Menumaster получили по итогам 2011 года. Данная награда вручается по итогам опроса клиентов, дилеров и экспертов ресторанного рынка.
Конвекция в духовке: 3 основных разновидности
Средняя духовка сегодня часто оборудована важной опцией, которая именуется режимом конвекции. Зачем она нужна в духовке, что это вообще и в чем ее польза заключается – об этом ниже по тексту.
Читайте также: Электрический или газовый духовой шкаф: 5 критериев выбора
Принцип работы духового шкафа
Начать стоит с простого: классические модели духовок состоят из одной или нескольких нагревателей (горелок), над которыми размещаются противни на разной высоте. В таких духовках пища подогревается только снизу, а наверху действует естественная конвекция, или разогретый воздух. Так блюдо часто пропекается неравномерно.
В инновационных моделях есть верхний нагрев. Например, в модели Zanussi ZZB 510301 X возможно сразу включить оба нагревателя. Дополнительный источник ускоряет и облегчает готовку. Во многих моделях – например, Gorenje BO625E01BK – есть гриль.
Виды духовых шкафов:
В разогреве духовки принимает участие вентилятор, который комбинирует потоки воздуха, горячие и холодные. В многофункциональных духовых шкафах верхний нагрев регулируется, и может включаться самостоятельно, или вместе с нижним.
Будет интересно почитать: Зависимая и независимая духовка: отличия 2 видов техники
Что такое конвекция?
Разобраться, что такое конвектор в духовке, несложно. Внутри шкафа легкий разогревшийся воздух занимает верхнюю часть, а холодный спускается ниже, где, в свою очередь, разогревается. И так – до полной стабилизации температурного режима. Такое явление называется природной или естественной конвекцией.
Даже в старых моделях печей она присутствует, но в естественном порядке процесс происходит очень медленно и не всегда справляется с прямым предназначением. Поэтому в современных вариантах – например, HANSA BOEI 68434 – она принудительная. В таких устройствах присутствует вентилятор, равномерно распределяющий воздух по рабочей камере.
Для чего конвекция в духовке? Ее наличие даст возможность:
- запекать большие и толстые куски мяса;
- получать хрустящую корочку;
- высушивать большое количество выделяющегося сока;
- разморозить овощи или мясо быстро.
Запущенный режим конвекции предполагает эффективное задействование полного объема духового шкафа. Можно ставить несколько противней, и не беспокоиться о равномерном пропекании блюда. Не обязательно запускать функцию при каждой готовке, но в случае выпекания тушки птицы или больших пирожков она незаменима.
Какие бывают конвекторы?
Конвекция присутствует решительно во всех разновидностях духовых шкафов. Она бывает:
- Естественной. Хорошо известна любому человеку, предусмотрена в стандартных духовках. Основана на природном процессе перемещения нагретовго и холодного воздуха по духовому шкафу. Не самый удобный в использовании вариант.
- Принудительной.
 Обустраивается в мультифункциональных моделях, типа Electrolux EOB55351AX. Тепло в таких духовках присутствует равномерно распределяется за счет вентилятора. Иногда он комбинируется с электрическими тэнами для полноценного пропекания.
Обустраивается в мультифункциональных моделях, типа Electrolux EOB55351AX. Тепло в таких духовках присутствует равномерно распределяется за счет вентилятора. Иногда он комбинируется с электрическими тэнами для полноценного пропекания. - Влажной или паровой. Предполагает насыщение паром воздуха внутри духовки. Так тесто поднимается лучше, пища не пересыхает и не поджаривается, сохраняя все полезные свойства.
Конвекция иногда комбинируется с грилем – например, как в модели PYRAMIDA F 105 S IX. В некоторых духовках конвекция объединена с усиленным грилем (это совмещение с верхним нагревом, для готовки больших порций и подрумянивания).
Это интересно: Топ-10 лучших производителей духовых шкафов
Ответ на вопрос, нужна ли конвекция в газовой или электрической духовке, довольно прост. Лишней она точно не будет, а вот полезной – еще как. Конвекция пригодится любителям здоровой еды и просто тем, кто любит, когда снаружи хрустит а внутри – сочно. Комбинируясь с разными видами нагрева, грилем, конвекция способствует более полной реализации возможностей мультифункционального духового шкафа. Благодаря этой опции выпекание любого блюда пройдет без хлопот.
Комбинируясь с разными видами нагрева, грилем, конвекция способствует более полной реализации возможностей мультифункционального духового шкафа. Благодаря этой опции выпекание любого блюда пройдет без хлопот.
Конвекция. Движение. Теплота
Конвекция
Но если вода такой плохой проводник тепла, то как же она нагревается в чайнике? Воздух еще хуже проводит тепло; тогда непонятно, почему во всех частях комнаты зимой устанавливается одинаковая температура.
Вода в чайнике быстро закипает из-за земного притяжения. Нижние слои воды, нагреваясь, расширяются, становятся легче и поднимаются кверху, а на их место поступает холодная вода. Быстрый нагрев происходит лишь благодаря конвекции (латинское слово, означающее «перемешивание»). Нагреть воду в чайнике, находящемся в межпланетной ракете, будет не так-то легко.
Еще об одном случае конвекции воды, не называя этого слова, мы говорили несколько раньше, объясняя, почему реки не промерзают до дна.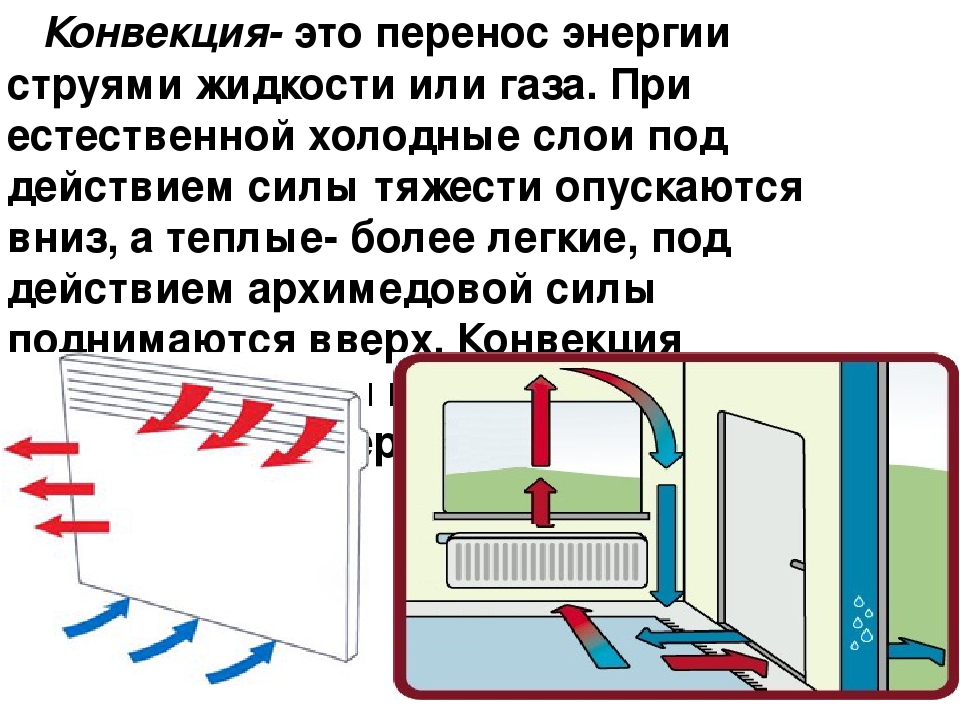
Почему батареи центрального отопления помещаются у пола, а форточки делаются в верхней части окна? Пожалуй, удобнее было бы открывать форточку, если бы она была внизу, а батареи, чтобы не мешались, было бы неплохо поместить под потолком.
Если бы мы послушались таких советов, то быстро бы обнаружили, что комната не прогревается батареей и не проветривается при открытой форточке.
С воздухом в комнате происходит то же самое, что и с водой в чайнике. Когда батарея центрального отопления включается, воздух в нижних слоях комнаты начинает нагреваться. Он расширяется, становится легче и поднимается кверху, к потолку. На его место приходят более тяжелые слои холодного воздуха. И они, нагревшись, уходят к потолку. Таким образом в комнате возникает непрерывное течение воздуха – теплого снизу вверх и холодного сверху вниз. Открывая форточку зимой, мы впускаем в комнату поток холодного воздуха. Он тяжелее комнатного и идет вниз, вытесняя теплый воздух, который поднимается кверху и уходит в форточку.
Керосиновая лампа хорошо разгорается лишь тогда, когда на нее надето высокое стекло. Не следует думать, что стекло нужно только для защиты пламени от ветра. И в самую тихую погоду яркость света сразу возрастает, как только на лампу надето стекло. Роль стекла состоит в том, что оно усиливает приток воздуха к пламени – создает тягу. Это происходит по той причине, что воздух внутри стекла, обедненный кислородом, затраченным на горение, быстро нагревается и идет кверху, а на его место поступает чистый холодный воздух через отверстия, сделанные в горелке лампы.
Чем выше стекло, тем лампа будет лучше гореть. Действительно, быстрота, с которой устремляется холодный воздух в горелку лампы, зависит от разности в весе нагретого столба воздуха в лампе и холодного воздуха вне лампы. Чем выше столб воздуха, тем больше будет эта разность весов, а с ней и быстрота перемешивания.
Поэтому и заводские трубы делают высокими. Для заводских топок нужен особенно сильный приток воздуха, нужна хорошая тяга. Она и достигается благодаря высоким трубам.
Она и достигается благодаря высоким трубам.
Отсутствие конвекции в лишенной тяжести ракете не позволит пользоваться спичками, лампами и газовыми горелками: продукты сгорания задушат пламя.
Воздух – плохой проводник; при его помощи мы можем сохранять тепло, но с одним условием: если мы избежим конвекции – перемешивания теплого и холодного воздуха, – которая сводит на нет теплоизоляционные свойства воздуха.
Устранение конвекции достигается применением разного рода пористых и волокнистых тел. Внутри таких тел воздуху трудно двигаться. Все подобные тела хороши как теплоизоляторы только благодаря своей способности удерживать слой воздуха. Теплопроводность же самих веществ волокна или стенок пор может быть не очень малой.
Хороша шуба из густого меха, содержащего как можно больше волокон; гагачий пух позволяет изготовлять теплые спальные мешки весом меньше полукилограмма из-за исключительной тонины своих волокон. Полкилограмма этого пуха могут «задержать» столько же воздуха, сколько десяток килограммов ватина.
Для уменьшения конвекции делают двойные рамы. Воздух между стеклами не участвует в перемешивании воздушных слоев, происходящем в комнате.
Наоборот, всякое движение воздуха усиливает перемешивание и увеличивает передачу тепла. Именно поэтому, когда нам нужно, чтобы тепло уходило побыстрее, мы обмахиваемся веером или включаем вентилятор. Поэтому на ветру и холоднее. Но если температура воздуха выше температуры нашего тела, то перемешивание приведет к обратному результату, и ветер ощущается, как горячее дыхание.
Задача парового котла состоит в том, чтобы как можно быстрее получать нагретый до нужной температуры пар. Естественной конвекции в поле тяжести для этого совершенно недостаточно. Поэтому создание интенсивной циркуляции воды и пара, приводящей к перемешиванию теплых и холодных слоев, является одной из основных задач при конструировании паровых котлов.
Смешанная свободная и вынужденная конвекция
Содержание:
Смешанная свободная и вынужденная конвекция
- Для вашего 7-10, свободная конвекция, влияние на подачу и передачу тепла силы Тома не было considered.
 In на самом деле, когда плотность изменяется с температурой, плавучесть возникает в нормальном потоке, и интересно знать, когда ею можно пренебречь, а когда нужно учитывать. Это соображение осложняется большим количеством влияний parameters. In помимо числа Рейнольдса и числа Прандтля, число глашофа также имеет важное значение.
In на самом деле, когда плотность изменяется с температурой, плавучесть возникает в нормальном потоке, и интересно знать, когда ею можно пренебречь, а когда нужно учитывать. Это соображение осложняется большим количеством влияний parameters. In помимо числа Рейнольдса и числа Прандтля, число глашофа также имеет важное значение.
Также важны параметры, описывающие геометрию границы и направление течения относительно гравитационного поля. По-видимому, наиболее полно исследован стимулированный поток через круглую трубу с осью, параллельной направлению ускорения силы тяжести, при этом средний поток направлен вверх или вниз. [224]. Влияние естественной конвекции на теплопередачу может не приниматься во внимание, если число Рейнольдса велико(и, следовательно, скорость потока велика) или число кузнечиков невелико.
Применение термодинамики для решения практических задач часто требует знания параметров, конкретизирующих свойства изучаемого объекта, то есть требуется математическая модель системы, с необходимой точностью описывающая её свойства.Людмила Фирмаль
С другой стороны, если число глашофа велико, а число Рейнольдса мало, то естественная конвекция должна быть доминирующей Факторы. Это проиллюстрировано на рисунке. В 11-15-вертикальная труба (крышка) с другим соотношением длины и диаметра и жидкость с другим числом Прандтля[L. 225].Принудительный поток через трубу будет в том же направлении, что и плавучесть потока у стенки трубы. Вы можете видеть, что область смешанного потока определяется как область, в которой теплопередача отличается более чем на 10%. Рис. 11-15.Режимы принудительного перемешивания и свободной конвекции[л. 373].
Теплопередача, полученная из зависимости вынужденного течения или свободной конвекции, на самом деле очень мала. Макс Адамс предложил правило, позволяющее определить теплообмен в области смешанного flow. In в этом случае вычисляется коэффициент теплопередачи вынужденной и свободной конвекции и используется большое значение. Измеренные значения, полученные для потока через вертикальную трубу, не отклоняются более чем на 25% от значений, рассчитанных по правилам Мак Адамса.
Задачи 11-1.Вычислите ламинарный перенос тепла свободной конвекцией вдоль плоской пластины, расположенной под углом к вертикальному направлению, используя интегральное уравнение пограничного слоя и тот же профиль скорости, что и§ 11-1. 11-2. Используйте интегральное уравнение пограничного слоя и профиль скорости, используемые в 11-1 для расчета коэффициента ламинарного свободного конвективного теплообмена вокруг горизонтального цилиндра кольцевого сечения.
- Предположим, что толщина пограничного слоя меньше диаметра цилиндра. 11-3.By эффект естественной конвекции, вызванной центробежной силой, вычисляют по локальному коэффициенту теплопередачи на поверхности охлаждающего воздушного канала в полой лопатке газовой турбины. Поскольку вынужденный поток воздуха при атмосферном давлении и температуре 260 ° С через проход очень мал, то влияние на конвективный теплообмен предполагается незначительным. Температура поверхности прохода составит » 538 В С.
 охлаждающие каналы расположены по оси, параллельной оси вращения, длиной 5,08 см, расстоянием от оси 38,1 см.
охлаждающие каналы расположены по оси, параллельной оси вращения, длиной 5,08 см, расстоянием от оси 38,1 см.
Лопатка крепится к турбинному колесу, которое вращается со скоростью 10 000 об / мин! В этом расчете мы предполагаем, что поверхность прохода можно считать плоской бритвой-ржавчиной, на которую действует центробежная сила. -Не принимай во внимание силу Кориолиса. 11-4. Используя расчеты, кратко описанные в § 11-2, выведем уравнение турбулентного свободного конвективного теплообмена на вертикальной пластине(11-16). 11-5.Теплопроводность газа часто измеряется методом Сазерленда путем встраивания платиновой проволоки вдоль оси капиллярной трубки, заполненной исследуемым газом. Проволока нагревается электрически, труба охлаждается снаружи, измеряется тепловой поток, температура проволоки и трубы.
Выбор независимых переменных для калорического уравнения состояния, теоретически не имеющий принципиального значения, важен с практической точки зрения: удобнее иметь дело с непосредственно измеримыми величинами типа температуры и давления.Людмила Фирмаль
Теплопроводность рассчитывается в предположении, что тепло от теплопроводности излучается от провода в трубку. Если желательно измерить теплопроводность водяного пара до давления 150 бар, то во избежание ошибок, обусловленных естественной конвекцией, определяют диаметр капилляра. (Используйте данные приложения для определения характеристик.!)Для этого используйте схему. Ил-14.Разница в температуры 5.6°C между трубкой и проводом поддержана. 11-6.
Температура плоских стенок сосуда составляет 93°с, изолированных 3 слоями алюминиевой фольги.1 слой находится на стене, еще 1 слой находится на расстоянии 1,25 см, соответственно, образуя 2 пространства. Снаружи изоляция охлаждается до 37,5°C окружающим воздухом. Какой температуры будет фольга пластины в середине быть? Сколько стоит тепловой поток в час на квадратный метр через изоляцию? Не учитывайте излучаемый теплообмен. 11-7.In в случае задачи 11-3 условия охлаждения воздуха, влиянием естественной конвекции на теплообмен можно пренебречь? (Предполагается, что гидравлический диаметр воздушного канала составляет 1 см. )
)
Смотрите также:
Коэффициент конвективной теплопередачи — обзор
Оцените температуру воздуха на выходе и эффективность коллектора, показанного на рис. 3.30, для следующих характеристик коллектора:
Ширина коллектора, Вт = 1,2 м.
Длина коллектора, L = 4 м.
Глубина воздушного канала, с = 15 мм.
Полная инсоляция, G т = 890 Вт / м 2
Температура окружающей среды, T a = 15 ° C = 288 K.
Эффективное (τα) = 0,90.
Коэффициент теплопотери, U L = 6,5 Вт / м 2 -K.
Коэффициент излучения пластины поглотителя, ε p = 0,92.
Коэффициент излучения задней пластины, ε b = 0,92.
Массовый расход воздуха = 0,06 кг / с.
Температура воздуха на входе, T i = 50 ° C = 323 K.
Решение
Здесь нам нужно начать с принятия значений для T p и T b . Для экономии времени подобраны правильные значения; но в реальной ситуации решение нужно искать путем итераций. Предполагаемые значения: T p = 340 K и T b = 334 K (они должны быть в пределах 10 K). По этим двум температурам можно определить среднюю температуру воздуха:
4 (Tm, воздух) 3 = (Tp + Tb) (Tp2 + Tb2)
, откуда
Tm, воздух = (Tp + Tb) (Tp2 + Tb2) 43 = (340 + 334) (3402 + 3342) 43 = 337 K
Коэффициент теплопередачи излучения от поглотителя к задней пластине равен
час, p-g2 = σ ( Tp + Tb) (Tp2 + Tb2) (1 / ɛp) + (1 / ɛb) -1 = (5.67 × 10-8) (340 + 334) (3402 + 3342) (1 / 0,92) + (1 / 0,92) -1 = 7,395 Вт / м2-К
От T м , воздух , следующие свойства воздуха можно получить из Приложения 5:
μ = 2,051 × 10-5 кг / м-ск = 0,029 Вт / м-Kcp = 1008 Дж / кг-K
Из гидродинамики гидравлический диаметр воздушный канал равен
D = 4 (Площадь поперечного сечения потока, смоченный периметр) = 4 (Ws2W) = 2s = 2 × 0,015 = 0,03
Число Рейнольдса равно
Re = ρVDμ = m˙DAμ = 0. 06 × 0,03 (1,2 × 0,015) × 2,051 × 10-5 = 4875,5
06 × 0,03 (1,2 × 0,015) × 2,051 × 10-5 = 4875,5
Следовательно, поток является турбулентным, для которого применимо следующее уравнение: Nu = 0,0158 (Re) 0,8 . Так как Nu = ( h c D ) / k , коэффициент конвективной теплопередачи определяется как
hc, pa = hc, ba = (kD) 0,0158 (Re) 0,8 = (0,0290,03) 0,0158 (4875,5) 0,8 = 13,625 Вт / м2-К
Из уравнения. (3,69),
h = hc, p-a + 1 (1 / hc, ba) + (1 / hr, pb) = 13,625 + 1 (1 / 13,625) + (1 / 7,395) = 18,4 Вт / м2-К
Из ур.(3,72),
F ′ = hh + UL = 18,418,4 + 6,5 = 0,739
Поглощенное солнечное излучение составляет
S = Gt (τα) = 890 × 0,9 = 801 Вт / м2
Из уравнения. (3,74),
To = Ti + 1UL [S-UL (Ti-Ta)] [1-exp (-AcULF′m˙cp)] = 323+ (16,5) [801-6,5 (323-288)] [1-exp (- (1,2 × 4) × 6,5 × 0,7390,06 × 1007)] = 351 K
Следовательно, средняя температура воздуха составляет ½ (351 + 323) = 337 K, что равно значению предполагалось раньше. Если есть разница в двух средних значениях, требуется итерация. Для такого рода задач требуется всего одна итерация, чтобы найти правильное решение с использованием предполагаемых значений, которые дают новую среднюю температуру.
Если есть разница в двух средних значениях, требуется итерация. Для такого рода задач требуется всего одна итерация, чтобы найти правильное решение с использованием предполагаемых значений, которые дают новую среднюю температуру.
Из уравнения. (3,58),
FR = m˙cpAcUL {1-exp [-ULF’Acm˙cp]} = 0,06 × 1008 (1,2 × 4) × 6,5 {1-exp [-6,5 × 0,739 × (1,2 × 4) 0,06 × 1008]} = 0,614
Из уравнения. (3,76),
Qu = AcFR [S-UL (Ti-Ta)] = (1,2 × 4) × 0,614 [801-6,5 (323-288)] = 1690 Вт
Наконец, эффективность коллектора составляет
η = QuAcGt = 1690 (1,2 × 4) × 890 = 0,396
Конвективная теплопередача
Тепловая энергия, передаваемая между поверхностью и движущейся жидкостью с разными температурами, известна как конвекция .
На самом деле это комбинация диффузии и объемного движения молекул. Вблизи поверхности скорость жидкости мала, и преобладает диффузия. На расстоянии от поверхности объемное движение усиливает влияние и преобладает.
Конвективная теплопередача может быть
- принудительной или вспомогательной конвекцией
- естественной или свободной конвекцией
принудительной или вспомогательной конвекцией
принудительной конвекцией жидкости
принудительной конвекцией внешняя сила, такая как насос, вентилятор или смеситель.
Естественная или свободная конвекция
Естественная конвекция вызывается силами плавучести из-за разницы плотности, вызванной колебаниями температуры в жидкости. При нагревании изменение плотности в пограничном слое приведет к тому, что жидкость поднимется и будет заменена более холодной жидкостью, которая также будет нагреваться и подниматься. Это продолжающееся явление называется свободной или естественной конвекцией.
Процессы кипения или конденсации также называют конвективными процессами теплопередачи.
- Теплопередача на единицу поверхности за счет конвекции была впервые описана Ньютоном, и это соотношение известно как Закон охлаждения Ньютона .

Уравнение конвекции может быть выражено как:
q = h c A dT (1)
где
q = теплопередача за единицу времени (Вт, БТЕ / ч)
A = площадь теплообмена поверхности (м 2 , фут 2 )
ч c = коэффициент конвективной теплопередачи процесса ( Вт / (м 2o C, Btu / (фут 2 h o F) )
dT = разница температур между поверхностью и основной жидкостью ( o C, F)
Коэффициенты теплопередачи — единицы
Коэффициенты конвективной теплопередачи
Коэффициенты конвективной теплопередачи — ч c — в зависимости от t тип среды, будь то газ или жидкость, и свойства потока, такие как скорость, вязкость и другие свойства, зависящие от потока и температуры.
Типичные коэффициенты конвективной теплопередачи для некоторых распространенных приложений с потоком жидкости:
- Свободная конвекция — воздух, газы и сухие пары: 0,5 — 1000 (Вт / (м 2 K))
- Свободная конвекция — вода и жидкости: 50 — 3000 (Вт / (м 2 K))
- Принудительная конвекция — воздух, газы и сухие пары: 10 — 1000 (Вт / (м 2 K))
- Принудительная конвекция — вода и жидкости: 50 — 10000 (Вт / (м 2 K))
- Принудительная конвекция — жидкие металлы: 5000 — 40000 (Вт / (м 2 K))
- Кипящая вода: 3.000 — 100,000 (Вт / (м 2 K))
- Водяной пар конденсата: 5.000 — 100,000 (Вт / (м 2 K))
Коэффициент конвективной теплопередачи для воздуха
Коэффициент конвективной теплопередачи для потока воздуха может быть приблизительно равен
ч c = 10,45 — v + 10 v 1/2 (2)
, где
h c = коэффициент теплопередачи (кКал / м 2 ч ° C)
v = относительная скорость между поверхностью объекта и воздухом (м / с)
Начиная с
1 ккал / м 2 ч ° С = 1. 16 Вт / м 2 ° C
16 Вт / м 2 ° C
— (2) можно изменить на
ч cW = 12,12 — 1,16 v + 11,6 v 1/2 (2b)
где
ч cW = коэффициент теплопередачи (Вт / м 2 ° C )
Примечание! — это эмпирическое уравнение, которое может использоваться для скоростей от 2 до 20 м / с .
Пример — конвективная теплопередача
Жидкость течет по плоской поверхности размером 1 м на 1 м. Температура поверхности 50 o C , температура жидкости 20 o C и коэффициент конвективной теплопередачи 2000 Вт / м 2o С . Конвективный теплообмен между более горячей поверхностью и более холодным воздухом можно рассчитать как
q = (2000 Вт / (м 2o C)) ((1 м) (1 м)) ((50 o C) — (20 o C))
= 60000 (Вт)
= 60 (кВт)
Калькулятор конвективной теплопередачи
Диаграмма конвективной теплопередачи
Механизм по конвекции — Характеристики
Конвекция происходит посредством адвекции, диффузии или того и другого. Передача тепла за счет теплопроводности зависит от движущей «силы» разницы температур.
Передача тепла за счет теплопроводности зависит от движущей «силы» разницы температур.Проводимость и конвекция похожи в том, что оба механизма требуют наличия материальной среды (по сравнению с тепловым излучением). С другой стороны, они отличаются тем, что конвекция требует наличия движения жидкости.
В теплопроводности энергия передается в виде тепла либо за счет миграции свободных электронов , либо за счет волн колебаний решетки (фононов). Нет движения массы в направлении потока энергии. Передача тепла за счет проводимости зависит от движущей «силы» разности температур . Проводимость и конвекция похожи в том, что оба механизма требуют наличия материальной среды (по сравнению с тепловым излучением). С другой стороны, они отличаются тем, что конвекция требует наличия движения жидкости.
Следует подчеркнуть , на поверхности поток энергии происходит исключительно за счет проводимости, даже за счет проводимости. Это связано с тем, что на поверхности теплопередачи всегда имеется тонкий застойный слой пленки жидкости . Но в следующих слоях происходит как проводимость, так и диффузионно-массовое движение на молекулярном или макроскопическом уровне. Из-за движения массы скорость передачи энергии выше. Чем выше скорость движения массы, тем тоньше будет слой застойной пленки жидкости и выше будет скорость теплового потока.
Это связано с тем, что на поверхности теплопередачи всегда имеется тонкий застойный слой пленки жидкости . Но в следующих слоях происходит как проводимость, так и диффузионно-массовое движение на молекулярном или макроскопическом уровне. Из-за движения массы скорость передачи энергии выше. Чем выше скорость движения массы, тем тоньше будет слой застойной пленки жидкости и выше будет скорость теплового потока.
Следует отметить, что пузырьковое кипение на поверхности эффективно разрушает этот застойный слой и, следовательно, пузырьковое кипение значительно увеличивает способность поверхности передавать тепловую энергию объемной жидкости.
Как было написано, теплопередача через жидкость происходит за счет конвекции при наличии движения массы и за счет теплопроводности при ее отсутствии. Следовательно, теплопроводность в жидкости можно рассматривать как предельный случай конвекции, соответствующий случаю покоящейся жидкости.
Конвекция как проводимость с движением жидкости
Некоторые эксперты не считают конвекцию фундаментальным механизмом теплопередачи, поскольку это, по сути, теплопроводность в присутствии движения жидкости.Они считают, что это особый случай теплопроводности , известный как «теплопроводность с движением жидкости ». С другой стороны, практично, , признать конвекцию отдельным механизмом теплопередачи, несмотря на веские аргументы об обратном.
Граничный слой скорости
В общем, когда жидкость течет по неподвижной поверхности , например плоская плита, русло реки или стенка трубы, жидкость, соприкасающаяся с поверхностью, доводится до упора под действием напряжения сдвига к стене.Область, в которой поток регулируется от нулевой скорости у стенки до максимальной в основном потоке потока, называется пограничным слоем . Концепция пограничных слоев важна во всей динамике вязкой жидкости, а также в теории теплопередачи.
Основные характеристики всех ламинарных и турбулентных пограничных слоев показаны в развивающемся потоке над плоской пластиной. Этапы формирования пограничного слоя показаны на рисунке ниже:
Пограничные слои могут быть либо ламинарными , либо турбулентными в зависимости от значения числа Рейнольдса .
См. Также: Граничный слой
Термический пограничный слой
Точно так же, как пограничный слой со скоростью развивается, когда есть поток жидкости по поверхности, тепловой пограничный слой должен развиваться, если объемная температура и температура поверхности различаются. Рассмотрим обтекание плоской изотермической пластины при постоянной температуре T стенка . На передней кромке профиль температуры однороден с T навалом . Частицы жидкости, которые контактируют с пластиной, достигают теплового равновесия при температуре поверхности пластины. В этот момент поток энергии происходит на поверхности исключительно за счет проводимости . Эти частицы обмениваются энергией с частицами в прилегающем слое жидкости (посредством проводимости и диффузии), и в жидкости возникают градиенты температуры. Область жидкости, в которой существуют эти температурные градиенты, представляет собой тепловой пограничный слой . Его толщина , δ t , как правило, определяется как расстояние от тела, на котором температура составляет 99% от температуры невязкого раствора.По мере удаления от передней кромки эффекты теплопередачи все глубже проникают в поток и тепловой пограничный слой нарастает.
В этот момент поток энергии происходит на поверхности исключительно за счет проводимости . Эти частицы обмениваются энергией с частицами в прилегающем слое жидкости (посредством проводимости и диффузии), и в жидкости возникают градиенты температуры. Область жидкости, в которой существуют эти температурные градиенты, представляет собой тепловой пограничный слой . Его толщина , δ t , как правило, определяется как расстояние от тела, на котором температура составляет 99% от температуры невязкого раствора.По мере удаления от передней кромки эффекты теплопередачи все глубже проникают в поток и тепловой пограничный слой нарастает. Отношение этих двух толщин (скорости и теплового пограничного слоя) определяется числом Прандтля, которое определяется как отношение к коэффициенту диффузии по импульсу к коэффициенту температуропроводности . Число Прандтля, равное единице, означает, что импульс и коэффициент температуропроводности сравнимы, а пограничные слои скорости и тепла почти совпадают. Если число Прандтля меньше 1, что имеет место для воздуха при стандартных условиях, тепловой пограничный слой толще, чем скоростной пограничный слой. Если число Прандтля больше 1, тепловой пограничный слой тоньше, чем скоростной пограничный слой. Воздух при комнатной температуре имеет число Прандтля , равное 0,71 , а для воды при 18 ° C — около 7,56 , что означает, что коэффициент температуропроводности более доминирующий для воздуха, чем для воды.
Если число Прандтля меньше 1, что имеет место для воздуха при стандартных условиях, тепловой пограничный слой толще, чем скоростной пограничный слой. Если число Прандтля больше 1, тепловой пограничный слой тоньше, чем скоростной пограничный слой. Воздух при комнатной температуре имеет число Прандтля , равное 0,71 , а для воды при 18 ° C — около 7,56 , что означает, что коэффициент температуропроводности более доминирующий для воздуха, чем для воды.
Так же, как для числа Прандтля , число Льюиса физически связывает относительную толщину теплового слоя и пограничного слоя массопереноса (концентрации).Число Шмидта физически связывает относительную толщину пограничного слоя скорости и пограничного слоя массопереноса (концентрации).
, где n = 1/3 для большинства приложений во всех трех отношениях. Эти соотношения, как правило, применимы только для ламинарного потока и не применимы к турбулентным пограничным слоям, поскольку турбулентное перемешивание в этом случае может доминировать над диффузионными процессами.
Теплопередача за счет конвекции сложнее проанализировать, чем теплопередачу за счет теплопроводности, потому что никакое отдельное свойство теплопередающей среды, такое как теплопроводность, не может быть определено для описания механизма. Конвективная теплопередача осложняется тем фактом, что она включает движение жидкости, а также теплопроводность . Теплопередача за счет конвекции меняется от ситуации к ситуации (в зависимости от условий потока жидкости), и это часто связано с режимом потока жидкости. При принудительной конвекции скорость передачи тепла через жидкость намного выше за счет конвекции, чем за счет теплопроводности.
На практике анализ теплопередачи за счет конвекции обрабатывается эмпирически (путем прямого экспериментального наблюдения).Большинство проблем можно решить с помощью так называемых характеристических чисел (например, число Нуссельта ). Характеристические числа являются безразмерными числами, используемыми для описания характера теплопередачи и могут использоваться для сравнения реальной ситуации (например, теплопередача в трубе) с мелкомасштабной моделью . Опыт показывает, что конвекционная теплопередача сильно зависит от свойств жидкости , динамической вязкости , теплопроводности , плотности и удельной теплоемкости , а также от скорости жидкости .Это также зависит от геометрии и шероховатости твердой поверхности в дополнение к типу потока жидкости. Все эти условия особенно сказываются на застойной пленке толщиной .
Опыт показывает, что конвекционная теплопередача сильно зависит от свойств жидкости , динамической вязкости , теплопроводности , плотности и удельной теплоемкости , а также от скорости жидкости .Это также зависит от геометрии и шероховатости твердой поверхности в дополнение к типу потока жидкости. Все эти условия особенно сказываются на застойной пленке толщиной .
Конвекция включает передачу тепла между поверхностью с заданной температурой (T , стенка ) и жидкостью с объемной температурой (T b ). Точное определение объемной температуры (T b ) варьируется в зависимости от деталей ситуации.
- Для потока, прилегающего к горячей или холодной поверхности, T b — это температура жидкости «далеко» от поверхности.
- Для кипения или конденсации T b — это температура насыщения жидкости.
- Для потока в трубе T b — это средняя температура, измеренная в определенном поперечном сечении трубы.

Ссылки:
Теплопередача:- Основы тепломассообмена, 7-е издание. Теодор Л. Бергман, Эдриенн С. Лавин, Фрэнк П. Инкропера. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Тепло- и массообмен.Юнус А. Ценгель. McGraw-Hill Education, 2011. ISBN: 9780071077866.
- Основы тепломассообмена. К. П. Котандараман. New Age International, 2006, ISBN: 9788122417722.
- Министерство энергетики США, термодинамики, теплопередачи и потока жидкости. Справочник Министерства энергетики США, том 2, 3 мая 2016 г.
Ядерная и реакторная физика:
- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Аддисон-Уэсли, Ридинг, Массачусетс (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную инженерию, 3-е изд., Прентис-Холл, 2001, ISBN: 0-201-82498-1.
- У. М. Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Гласстон, Сесонске. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4-е издание, 1994 г., ISBN: 978-0412985317
- W.S.C. Уильямс. Ядерная физика и физика элементарных частиц. Clarendon Press; 1 издание, 1991 г., ISBN: 978-0198520467
- G.Р.Кипин. Физика ядерной кинетики. Аддисон-Уэсли Паб. Co; 1-е издание, 1965 г.
- Роберт Рид Берн, Введение в эксплуатацию ядерных реакторов, 1988 г.
- Министерство энергетики, ядерной физики и теории реакторов США. Справочник по основам DOE, тома 1 и 2. Январь 1993 г.
- Пол Ройсс, Нейтронная физика. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Введение в статику ядерных реакторов, Американское ядерное общество, пересмотренное издание (1989), 1989, ISBN: 0-894-48033-2.
- К. О. Отт, Р. Дж. Нойхольд, Введение в динамику ядерных реакторов, Американское ядерное общество, 1985, ISBN: 0-894-48029-4.
- Д. Л. Хетрик, Динамика ядерных реакторов, Американское ядерное общество, 1993, ISBN: 0-894-48453-2.
- Э. Льюис, У. Ф. Миллер, Вычислительные методы переноса нейтронов, Американское ядерное общество, 1993, ISBN: 0-894-48452-4.
Множественные состояния и транспортные свойства турбулентности с двойной диффузной конвекцией
Значение
Когда два разных скаляра, которые одновременно влияют на плотность жидкости, испытывают соответствующие вертикальные градиенты, возникает турбулентность с двойной диффузией, которая значительно усиливает перемешивание.Такой процесс носит повсеместный характер. В океане DDC оказывает глубокое влияние на вертикальное перемешивание и вызывает интригующие термохалинные лестницы, а именно набор хорошо перемешанных конвекционных слоев, разделенных острыми границами раздела с очень высокими градиентами средней температуры и солености. Здесь мы проводим крупномасштабное численное моделирование таких течений в режиме аппликатуры, который обычно встречается в (суб) тропическом регионе. Мы показываем, что множественные состояния равновесия существуют в аппроксимирующих термохалинных лестницах с точно такими же фоновыми условиями, и разрабатываем законы масштабирования для описания потоков на стыках пальцев.
Abstract
Когда стратификация жидкости вызывается вертикальными градиентами двух скаляров с разной диффузионной способностью, может возникать двойная диффузионная конвекция (ДДК), которая играет решающую роль в перемешивании. Такой процесс существует во многих природных и инженерных средах. DDC присутствует повсеместно, особенно в океане, поскольку на плотность морской воды влияют температура и соленость. Наиболее интригующим явлением, вызванным DDC, является термохалинная лестница, то есть набор чередующихся хорошо перемешанных конвективных слоев и резких границ раздела с очень большими градиентами как температуры, так и солености.Здесь мы исследуем DDC и термохалинные лестницы в режиме солевого пальца, который происходит, когда теплая соленая вода находится над холодной более пресной водой и обычно наблюдается в (суб) тропических регионах. Проведя прямое численное моделирование для большого диапазона параметров, мы выявили, что существует несколько состояний равновесия при аппликатуре DDC и лестниц даже для одних и тех же параметров управления. Различные состояния могут быть установлены из разных начальных скалярных распределений или разных историй эволюции параметров потока.Гистерезис появляется при переходе от лестницы к интерфейсу с одним солевым пальцем. При одинаковом соотношении локальной плотности границы раздела соляных пальцев в однослойном состоянии генерируют потоки, сильно отличающиеся от потоков внутри лестничных клеток. Однако поток солености для всех границ раздела солевых пальцев следует той же зависимости от солености числа Рэлея слоя и может быть описан с помощью эффективного степенного масштабирования. Наши результаты имеют прямое применение к океаническим термохалинным лестницам.
Двойная диффузионная конвекция (DDC) относится к конвекционным потокам, управляемым плавучестью, где плотность жидкости зависит от двух скалярных компонентов. Наиболее важной земной средой, где встречается DDC, является океан, поскольку плотность морской воды зависит как от температуры, так и от солености. Благодаря основополагающей работе Стерна (1), теперь ясно, что DDC повсеместно распространены в океане (2) и имеют решающее значение для перемешивания океанов (3, 4). Одним из самых интригующих явлений, вызванных DDC, является термохалинная лестница, где средние вертикальные профили температуры и солености принимают отчетливые ступенчатые формы.Термохалинные лестницы широко распространены в океанах (5⇓⇓⇓⇓ – 10). Более того, DDC также играет значительную роль во многих других природных и инженерных средах, когда задействованы два разных скалярных компонента, например, в астрофизике (11⇓ – 13), геонауках (14⇓ – 16) и технологических процессах (17, 18). .
В частности, в (суб) тропическом океане средняя температура и соленость снижаются с глубиной в верхних слоях воды, и DDC обычно находится в режиме аппликатуры (1, 2), то есть поток управляется нестабильным градиентом солености и стабилизируется. по температурному градиенту.Термохалинные лестницы в этих регионах состоят из набора чередующихся полностью смешанных конвективных слоев и острых поверхностей стыка с пальчатыми структурами. Такие лестницы оказывают значительное влияние на диапикнальное перемешивание (8, 9) и могут даже ослаблять изменение климата океана (19).
Используя систему «соль-сахар», Кришнамурти успешно произвел аппликатурные лестницы из изначально линейных скалярных профилей между двумя резервуарами с постоянными концентрациями (20, 21). Эксперименты показали, что глобальные потоки сильно зависят от конкретной конфигурации лестниц, т.е.g., количество конвективных слоев и аппликатурных поверхностей. Недавно моделирование показало, что в трипериодической области интерфейс для пальцев может спонтанно превратиться в прочную лестницу с двумя равномерно расположенными интерфейсами для пальцев (22).
Ключевые вопросы при аппликатуре DDC включают законы потока, механизм формирования лестниц и вертикальные масштабы длины слоев. Обычно в качестве единственного управляющего параметра для потоков пальцевых структур принимают отношение плотностей Λ = βTΔT / βSΔS.Здесь ΔT и ΔS — две скалярные разности в слое жидкости; βT и βS — коэффициенты теплового расширения и сжатия солености соответственно. Эксперименты показывают, что толщина слоя также важна для потоков (20, 21, 23). Многие модели были разработаны для объяснения образования и типичных масштабов лестниц, таких как коллективная нестабильность (24, 25), термохалинное вторжение (26), скопление пальцев (27) и гамма-нестабильность (22, 28, 29), но однозначного ответа пока нет.
Здесь с помощью крупномасштабного прямого численного моделирования с полным разрешением мы обнаруживаем поразительные и неожиданные свойства аппликатурных лестниц. Мы используем многосеточный код, разработанный в нашей группе, который широко используется для конвективных и пристеночно-турбулентных потоков. Мы моделируем слой жидкости, ограниченный двумя параллельными пластинами, перпендикулярными направлению силы тяжести. Две пластины являются нескользкими и разделены высотой H. Фиксированные разницы температуры и солености, обозначаемые ΔT и ΔS, поддерживаются в слое жидкости, при этом верхняя пластина имеет более высокую температуру и соленость.Для развития аппликатуры DDC коэффициент температуропроводности κT должен быть больше, чем у солености κS. Здесь мы положили Pr = ν / κT = 7, где ν — кинематическая вязкость, т.е. типичное значение для (суб) тропического океана. Число Шмидта Sc = ν / κS имеет типичное значение 700. Такое высокое значение Sc недопустимо в наших трехмерных (3D) моделированиях из-за огромного количества требуемых вычислительных ресурсов, и мы должны выбрать меньшее значение Sc = 21. При конвекции Рэлея – Бенара (РБ) хорошо известно, что особенности потока совершенно нечувствительны к точному значению коэффициента диффузии, если он достаточно мал.Также для DDC это обычное лечение в предыдущих исследованиях, и сниженный Sc все еще может улавливать существенную динамику потока (22, 27).
Моделирование и эксперименты показали, что для слоя жидкости, ограниченного по вертикали двумя пластинами, как только интерфейс с одним пальцем занимает весь объем, он не разбивается на лестницы (20, 30). Также вдохновлен ранними экспериментами, в которых пальцы конечной длины могут расти из резкой границы раздела между двумя слоями с разной температурой и соленостью, например.г., см. исх. 31⇓ – 33, чтобы достичь возможного ступенчатого состояния, мы сначала вводим две острые границы раздела на двух пластинах со скалярными разностями ΔT / 2 и ΔS / 2. Нас интересует установившееся на основании этого статистически устойчивое состояние. Кроме того, мы зафиксировали коэффициент плотности Λ = 1,2, который находится в типичном диапазоне значений, обнаруженном в океане с аппликатурой DDC. Затем мы систематически увеличиваем соленое число Рэлея RaS = gβSΔSh4 / νκS, где g — ускорение свободного падения. Для каждого случая размер горизонтального домена выбирается намного больше, чем типичная ширина солевых пальцев.Поскольку солевые пальцы становятся более узкими с увеличением RaS, размер домена соответственно уменьшается.
Результаты
Множественные состояния в морфологии потока.
Сначала мы сосредоточимся на морфологии потока и глобальном потоке солености, которые измеряются числом Нуссельта NuS = (wS¯ − κS∂zS¯) / (κSΔSH − 1). Здесь полоса обозначает среднее значение по горизонтальным направлениям и по времени, w — вертикальная скорость, а ∂z — частная производная по вертикальной координате. Постепенно увеличиваем RaS со 108 до 1013; см. закрытые символы на рис.1. Когда RaS≤8 × 1010, пальцы в конечном итоге заполняют всю объемную область и образуют единый контакт пальца между двумя пограничными слоями, прилегающими к пластинам (Рис. 1 B и C ). Однако для немного большего RaS = 9 × 1010 хорошо перемешанный конвективный слой появляется между двумя интерфейсами пальцев (рис. 1 F ). В этом исследовании мы отличаем хорошо перемешанные конвективные слои от границ раздела пальцев по очень разным горизонтальным характерным масштабам длины и средним скалярным профилям.Как видно на рис. 1 F , в интерфейсах верхнего и нижнего пальцев структуры потока тонкие и более организованные, в то время как в среднем конвективном слое горизонтальный масштаб длины намного больше, и поток более хаотичный. Более того, средние значения обоих скаляров почти постоянны с высотой в конвективном слое, но имеют конечные градиенты внутри границ раздела пальцев.
Рис. 1.Глобальный поток солености NuS (компенсированный RaS − 1/3) и различные состояния потока. Изолинии на вертикальных плоскостях, помеченные соответствующим числом Рэлея солености RaS, отображают вертикальную скорость, нормированную на среднеквадратичное значение.Сплошными символами отмечены случаи с изначально однородным скалярным распределением. ( A ) Увеличенный вид области 7 × 1010≤RaS≤1,15 × 1011. ( B и C ) Интерфейс с одним пальцем получается, когда RaS≤8 × 1010 (оранжевые квадраты). ( D и E ) Интерфейс с одним пальцем сохраняется, когда RaS постепенно увеличивается с 8 × 1010 до 1 × 1012 (незакрашенные фиолетовые ромбы). ( F и G ) Однако для RaS≥9 × 1010 возникает трехслойное состояние с конвективным слоем между двумя интерфейсами пальцев, если начать моделирование с однородных скалярных распределений (зеленые кружки).Когда RaS уменьшается с 9 × 1010 до 8 × 1010, трехуровневая лестница в F переходит к интерфейсу с одним пальцем в C . Все контуры имеют одинаковую цветовую карту и при моделировании показаны с их фактическим соотношением сторон.
Изменение морфологии потока происходит при некотором критическом RaSc между 8 × 1010 и 9 × 1010. Переход очень резкий, поскольку для RaS = 9 × 1010 толщина каждого контакта пальцев составляет примерно 25% от общей высоты H. При дальнейшем увеличении RaS конвективный слой в середине становится выше и занимает больше места.Наиболее поразительный результат состоит в том, что гистерезис возникает во время изменения морфологии потока и существует несколько состояний, когда RaS> RaSc. Такой гистерезис наглядно показан на рис. 1 A . Для трехслойной лестницы, показанной на рис. 1 F , если RaS уменьшается с 9 × 1010 до 8 × 1010, два контакта пальца вверху и внизу будут расти по высоте, и поток восстанавливает однослойное состояние, как показано на рис.1 С . Однако при увеличении RaS с 8 · 1010 до 9 · 1010 поток остается в однослойном состоянии и не разбивается на лестницы.Наше моделирование показывает, что такое однослойное состояние сохраняется даже при увеличении RaS до 1 × 1012, как показано светлыми ромбами на рис. 1 A . В полностью периодическом трехмерном моделировании (22) горизонтально однородные и вертикально квазипериодические моды неустойчивости могут непрерывно нарастать и в конечном итоге приводить к появлению лестниц. Напротив, мы всегда наблюдаем горизонтальный зональный поток, как в наших предыдущих 3D-симуляциях (30), но не образуем лестницы из состояния контакта с одним пальцем, даже после того, как симуляции были запущены в течение 15 000 безразмерных единиц времени.
Приведенные выше результаты показывают, что различные конечные состояния могут быть достигнуты за счет разной истории эволюции потока из-за гистерезиса системы. Кроме того, наше численное исследование показывает, что разные начальные условия могут приводить к разным конечным состояниям. Чтобы продемонстрировать это, мы запускаем моделирование при RaS = 1 × 1013, начиная с трех различных начальных распределений скаляров (рис. 2): на рис. 2 A — один однородный слой, ограниченный двумя острыми границами раздела на пластинах; 2 B — два однородных слоя с двумя граничными поверхностями и внутренним при z / H = 0.5; а на рис. 2 C — три однородных слоя с двумя граничными поверхностями и двумя внутренними при z / H = 0,3 и 0,7. В каждой из трех симуляций интерфейсы имеют сильные стороны, например, одинаковые скалярные различия. Остальные глобальные параметры управления одинаковы для трех случаев: действительно, лестницы разные.
Рис. 2.Несколько состояний из разных начальных скалярных распределений ( A — C ) Различные лестницы при RaS = 1013 по объемной визуализации аномалии солености и соответствующих средних скалярных профилей.Увеличенный вид одного внутреннего интерфейса пальца (отмечен черным прямоугольником в B ) предназначен для ( D ) аномалии солености, ( E ) температурной аномалии и ( F ) вертикальной скорости, нормированной ее среднеквадратичное значение. A — C имеют те же настройки цвета и непрозрачности, что и D . Все поля потока показаны с их фактическим соотношением сторон при моделировании.
Статистически стационарные состояния, являющиеся результатом трех начальных условий, показаны на рис.2 A — C по объемной визуализации аномалии солености S ′ = S − S¯ и средних профилей температуры и солености. Три лестницы демонстрируют различные комбинации конвекции и стыков пальцев. Специально для случая, показанного на рис. 2 C , все четыре контакта с пальцами создают одинаковый поток, поскольку поток статистически стационарный, но средний конвективный слой имеет большую толщину, чем верхний и нижний. Это указывает на то, что границы раздела пальцев с одинаковыми потоками могут поддерживать конвекционные слои с разной высотой.Структуры потока внутри одной из внутренних границ раздела пальцев выделены на рис. 2 D — F объемными изображениями аномалии солености, аномалии температуры T ′ = T − T¯ и вертикальной скорости. Несмотря на энергичные движения в соседних конвекционных слоях, относительно хорошо организованные вертикально выровненные пальцы отличаются друг от друга и выдерживают высокие скалярные градиенты внутри границ раздела пальцев.
Транспортные свойства.
Глобальный поток солености NuS сильно зависит от точной морфологии потока, как показано на рис.1 А . Для трех случаев, показанных на рис. 2, глобальные потоки также различны. Модель глобального потока может быть очень сложной, особенно учитывая множественные состояния потока. Поэтому в дальнейшем мы сосредоточимся на транспортных свойствах пальцевых интерфейсов. Мы классифицируем все интерфейсы пальцев в наших симуляциях на два разных типа. Тип I — это те, которые занимают всю площадь в однослойном состоянии, а тип II — это те, которые находятся внутри лестниц, либо рядом с границей, либо между двумя конвекционными слоями.Край межпальцевых границ идентифицируется по локальному максимуму среднеквадратичного значения горизонтальной скорости. Отношение кажущейся плотности границы раздела пальцев можно рассчитать как Λapp = (βT∂zT¯) / (βS∂zS¯). Здесь и далее кажущиеся значения относятся к значениям, измеренным по полю потока во время статистически устойчивой стадии. Хотя общий коэффициент плотности установлен на уровне 1,2, расчеты показывают, что Λapp составляет примерно от 1,5 до 2,2.
На рис. 3 A и B показаны зависимости от Λapp безразмерного конвективного потока солености NuSapp = wS¯ / (κS∂zS¯) и отношения потоков γapp = (βTwT¯) / (βSwS¯) .Коэффициент потока измеряет отношение аномалии плотности, вызванной теплопередачей, к аномалии солености. Ясно, что слои разных типов могут генерировать очень разные потоки даже при одинаковом соотношении плотностей. Например, при Λapp≈1,5 интерфейсы пальцев типа I имеют намного больший Nusapp и меньший γapp, чем у слоев типа II. Примечательно, что транспортные свойства пальцевых интерфейсов типа I, а именно NuSapp и γapp, очень похожи на свойства, полученные при полностью периодическом моделировании (22), как показано красными квадратами и серыми крестиками на рис.3 A и B . Таким образом, когда интерфейс пальца занимает всю область, твердая граница оказывает лишь незначительное влияние на потоки. Однако, если мы построим график зависимости потока солености от кажущегося числа Рэлея RaSapp = g βS ∂zS¯ (hf) 4 / (νκS), NuSapp будет следовать единой тенденции для всех интерфейсов пальцев, несмотря на их разные типы (рис. 3 C ) . Здесь hf — высота пальцевых интерфейсов. Поток солености можно описать эффективным масштабным законом NuSapp∼2,19 (RaSapp) 0.176. Единственная зависимость NuSapp от RaSapp, а не от Λapp предполагает, что поток солености является функцией как локальных скалярных градиентов, так и толщины границ раздела пальцев. Тот факт, что поток зависит как от скалярного градиента, так и от толщины, также наблюдался в предыдущих экспериментах (например, см. Ссылки 20 и 23).
Рис. 3.Транспортные свойства для пальцевых интерфейсов типа I (красные квадраты) и типа II (синие кружки). ( A ) Кажущаяся соленость, число Нуссельта NuSapp и ( B ) отношение кажущейся плотности потока γapp в зависимости от отношения кажущейся плотности Λapp.Серые крестики показывают результаты полностью периодического моделирования из исх. 22 для сравнения. ( C ) NuSapp в зависимости от кажущейся солености числа Рэлея RaSapp. Пунктирной линией отмечен эффективный закон масштабирования NuSapp ~ 2,19 (RaSapp) 0,176. Планки погрешностей показывают среднеквадратичное значение временного колебания.
Следует отметить, что эффективный показатель масштабирования 0,176 на рис. 3 C очень близок к значению, найденному в экспериментах с солью и сахаром, где оно составляет от 0,18 до 0,19 (20).Однако эти значения значительно ниже по сравнению с законом 4/3, т.е. βSwS¯∼ (βSΔSf) 4/3 (31, 33), поскольку закон 4/3 соответствует масштабированию числа Нуссельта NuSf = wS¯ / ( κSΔSf / hf) ∼ (ΔSf) 1 / 3∼ (RaSf) 1/3 для постоянной толщины границы раздела hf. Одна из возможных причин заключается в том, что в экспериментах (31, 33) толщина h со временем увеличивается. Хотя проводящий поток κSΔSf / hf, который используется для обезразмеривания в определении NuSf, уменьшается со временем, число Рэлея RaSf увеличивается намного быстрее, а именно как ∼ (hf) 3.Следовательно, закон 4/3 в экспериментах должен быть преобразован в степенной закон масштабирования Nusf∼ (RaSf) α с α меньше 1/3.
Эффекты числа Шмидта.
Приведенные выше данные о множественных состояниях и потоках аппликатуры лестниц дают представление о термохалинных лестницах в океанах. Однако, чтобы напрямую применить наши результаты к реальным наблюдениям за океаном, необходимо прояснить влияние числа Шмидта, поскольку в наших 3D-симуляциях используется Sc = 21, что намного меньше, чем те, которые обычно наблюдаются в океане, которые составляют Sc = 700.К сожалению, прямое численное 3D-моделирование невозможно для таких высоких значений Sc из-за необходимости в больших сетках. Чтобы проверить надежность наших результатов и их применимость в океанской среде, мы провели двухмерное (2D) моделирование для трех различных чисел Шмидта, как показано на рис. 4 A . В частности, для каждого Sc мы провели серию моделирования при фиксированном Λ = 1,2 и постепенном увеличении RaS. Исходные скалярные распределения такие же, как для случаев, обозначенных сплошными символами на рис.1, т.е. две острые границы раздела на верхней и нижней пластинах с равномерным распределением между ними.
Рис. 4.Пространства параметров и транспорт пальцевых интерфейсов для 2D-моделирования. ( A ) Пространство параметров, смоделированное в 2D-моделировании, с однопальцевыми слоями, отмеченными оранжевыми квадратами, а лестничные клетки — зелеными квадратами. Черная стрелка указывает переход RaS для 3D-моделирования с Sc = 21. ( B ) Потоки солености NuSapp по сравнению с RaSapp для пальцевых интерфейсов типа I (красные квадраты) и типа II (синие кружки).Для каждого Sc данные могут быть хорошо описаны с помощью эффективных степенных масштабных соотношений с наклонами 0,232 для Sc = 21, 0,229 для Sc = 70 и 0,220 для Sc = 700. В B интерфейсы пальцев типа I (отмечены красными квадратами) взяты из корпусов, отмеченных оранжевыми квадратами в A , а интерфейсы пальцев типа II (отмечены синими кружками) взяты из корпусов, отмеченных зелеными кружками на рисунке. А .
Наши результаты показывают сильное сходство для разных чисел Шмидта, а также между 2D и 3D потоками.Переход из однослойного состояния в трехуровневую лестницу всегда происходит при превышении RaS критического значения. Однако критическое значение RaSc увеличивается с увеличением Sc. RaSc 2D результатов для Sc = 21 немного больше, чем у 3D. При Sc = 700 морской воды RaSc составляет от 1012 до 4 × 1012 в 2D-моделировании. Более того, для каждого Sc зависимость NuSapp от RaSapp для всех пальцевых интерфейсов разных типов может быть хорошо описана с помощью масштабирования по эффективному степенному закону.Показатель степени немного уменьшается с 0,232 для Sc = 21 до 0,220 для Sc = 700.
Для Sc = 21 показатель степени в эффективном законе масштабирования для 2D-результатов примерно на 30% больше, чем для 3D-результатов. Хорошо известно, что в односкалярной RB-конвекции показатели степени очень похожи между результатами 2D и 3D. Точные причины разницы между потоками DDC и RB и показателями двухмерных и трехмерных интерфейсов пальцев не ясны. Одним из возможных аргументов может быть различная морфология основных структур потока в балке.В потоках RB плоские крупномасштабные циркуляции существуют как в 2D, так и в 3D схемах. Поскольку крупномасштабная циркуляция преобладает над потоком в объеме, разумно, что показатели масштабирования аналогичны. Для пальцевых интерфейсов в DDC основными структурами, ответственными за перенос солености, являются вертикально ориентированные пальцы. В трехмерном моделировании пальцы имеют круглое поперечное сечение, в то время как для двухмерных случаев пальцы фактически представляют собой плиты с бесконечной длиной в третьем направлении. Поперечные сечения различаются, и соленость затем передается с разной скоростью для 2D и 3D пальцев.Следовательно, можно ожидать различных показателей масштабирования.
Обсуждения
Множественные состояния термохалинных лестниц, представленные здесь, явно являются следствием различных типов пальцевых интерфейсов. В наших симуляциях два интерфейса пальцев могут сливаться в один при изменении глобальных параметров. Когда интерфейс с одним пальцем занимает весь домен, мы никогда не наблюдаем его разделения на лестницу. Подобные явления были зарегистрированы для вертикально ограниченного потока DDC соль-сахар (20).В полностью периодической области состояние интерфейса с одним пальцем нестабильно по отношению к некоторым горизонтально инвариантным и вертикально квазипериодическим режимам, которые вызывают появление спонтанного наслоения (22). Такой механизм нестабильности, по-видимому, не существует в вертикально ограниченной конфигурации. Эти несоответствия между различными областями потока и гистерезис, показанный на рис. 1 A , предполагают, что может существовать определенный механизм докритической нестабильности для перехода от интерфейса с одним пальцем к лестнице.Запуск спонтанного наслоения из интерфейса одного пальца в ограниченной области может потребовать возмущения конечной амплитуды или даже более высоких чисел Рэлея.
Наши результаты показывают, что интерфейсы пальцев разных типов демонстрируют очень разные транспортные свойства, даже если они имеют одинаковое соотношение локальной плотности. Потоки зависят как от локальных фоновых средних скалярных градиентов, так и от высоты границы раздела пальцев, т. Е. Локального числа Рэлея границ раздела пальцев.Одного отношения локальных плотностей недостаточно для описания потоков. Модификация обычно используемого закона градиента потока была предложена и протестирована для полностью периодической области (34). Другой связанный открытый вопрос — это то, что управляет высотой интерфейса для пальцев, особенно внутри лестничных клеток. Было разработано множество теорий, включая теорию коллективной неустойчивости (24) и недавнюю модель равновесного переноса (35). Применимость этих моделей будет предметом будущих исследований.
Наконец, текущие результаты имеют прямое влияние на океанические потоки DDC. Существование множества состояний подразумевает, что точная конфигурация термохалинных лестниц не только определяется фоновой средой, но и связана с историей эволюции. Глобальные потоки лестниц действительно зависят от точных комбинаций конвективных и аппликатурных слоев. Тем не менее, можно параметризовать потоки на стыках пальцев, используя как локальные градиенты, так и толщину слоя, как это было сделано для эффективных законов масштабирования, предложенных здесь.Их можно легко проверить с помощью данных наблюдений из океана.
Материалы и методы
Мы проводим прямое численное моделирование потока DDC между двумя параллельными пластинами, перпендикулярными направлению силы тяжести. Используется приближение Обербека – Буосинеска; т.е. плотность жидкости линейно зависит от двух скалярных компонент. Уравнение несжимаемой жидкости Навье – Стокса и два уравнения адвекции – диффузии для скаляров имеют вид ∂tui + uj∂jui = −∂ip + ν∂j2ui + gδi3 (βTT − βSS), [1] ∂tT + uj∂jT = κT∂j2T , [2] ∂tS + uj∂jS = κS∂j2S.[3] Здесь ui с i = 1,2,3 — три составляющие скорости, p — давление, ν — кинематическая вязкость, g — ускорение свободного падения, βT — коэффициент теплового расширения, βS — коэффициент сжатия солености, T и S — температура и соленость относительно их эталонных значений, а κT и κS — коэффициенты диффузии двух скаляров. Динамическая система дополнительно ограничена уравнением неразрывности ∂iui = 0. И на верхней, и на нижней пластинах мы используем условие прилипания для скорости и условие постоянного значения для двух скаляров.Таким образом, глобальные скалярные различия остаются постоянными по всему слою жидкости. В двух горизонтальных направлениях мы используем периодические условия.
Основные уравнения решаются численно с помощью конечно-разностной схемы второго порядка с методом дробных временных шагов. В частности, код использует метод двойного разрешения, чтобы эффективно работать со скалярной составляющей высокого числа Шмидта, и был тщательно протестирован на предмет конвективной турбулентности (36). Уравнения обезразмериваются высотой области H, скоростью свободного падения gβSΔSH и скалярными разностями ΔT и ΔS.Для всех симуляций размер сетки выбирается так, чтобы адекватно разрешить длину Колмогорова ηK = (ν3 / ϵu) 1/4 для импульсного поля и длину Бэтчелора ηB = (νκ2 / ϵu) 1/4 для каждого скалярного поля. Здесь ϵu — скорость вязкой диссипации.
Трехмерная визуализация создается с помощью программного обеспечения с открытым исходным кодом VisIt (37). Все необработанные данные моделирования хранятся в архиве голландского консорциума суперкомпьютеров SURFsara.
Благодарности
Ю.Ю. и W.C. выражаем признательность за поддержку грантов 91852107 и 91752202 Национального фонда естественных наук Китая за поддержку турбулентных структур.Ю.Ю. также признает частичную поддержку Программы стратегических приоритетных исследований Китайской академии наук, грант XDB42000000. Это исследование частично поддерживается Фондом фундаментальных исследований материи и Нидерландским центром многомасштабного каталитического преобразования энергии, программой Гравитационного совета Нидерландов (NWO), финансируемой Министерством образования, культуры и науки правительства Нидерландов. Вычислительные ресурсы предоставляются NWO в голландском консорциуме суперкомпьютеров SURFsara и партнерством по передовым вычислениям в Европе в итальянском консорциуме суперкомпьютеров Cineca в рамках проекта 2019204979.
Сноски
Авторы: Y.Y., R.V., and D.L. спланированное исследование; Y.Y., W.C., R.V. и D.L. проведенное исследование; Y.Y., W.C., R.V. и D.L. проанализированные данные; и Y.Y., W.C., R.V., and D.L. написал газету.
Авторы заявляют об отсутствии конкурирующей заинтересованности.
Эта статья представляет собой прямое представление PNAS.
Размещение данных: все необработанные данные моделирования хранятся в архиве голландского консорциума суперкомпьютеров SURFsara, а статистические данные используются для воспроизведения рис.1, 3 и 4 доступны в наборах данных S1 – S3.
Эта статья содержит вспомогательную информацию в Интернете по адресу https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2005669117/-/DCSupplemental.
Какой фактор влияет на коэффициент теплопередачи при тепловой конвекции? — Mvorganizing.org
Какой фактор влияет на коэффициент теплопередачи при тепловой конвекции?
Коэффициент теплопередачи зависит как от тепловых свойств среды, гидродинамических характеристик ее потока, так и от гидродинамических и тепловых граничных условий.
От чего зависит коэффициент конвективной теплоотдачи?
Соответственно, коэффициент конвективной теплопередачи зависит от (1) теплофизических свойств жидкости и (2) скорости жидкости.
Как влияет коэффициент конвективной теплопередачи на эффективность?
Результаты показывают, что (а) чем больше значение коэффициента теплопередачи конвекции h, тем меньше эффективность плавников и эффективность плавников (б) В условиях нестационарного состояния эффективность и эффективность зависят от значения плотности, удельной теплоемкости. , коэффициент теплопроводности и…
Что такое конвективная теплопередача?
При заданной разнице температур между горячими и холодными поверхностями увеличение коэффициента конвективной теплопередачи снижает тепловой КПД ТЭГ.
Как увеличить коэффициент теплопередачи?
Для увеличения скорости теплопередачи скорость через рубашку может быть увеличена за счет рециркуляции охлаждающей или нагревающей жидкости. Для простых рубашек без перегородок теплопередача будет в основном за счет естественной конвекции, а коэффициент теплопередачи будет составлять от 200 до 400 Вт / м2 ° C.
Меняется ли коэффициент теплопередачи с температурой?
Это, в свою очередь, влияет на коэффициент теплопередачи, несмотря на возможную одинаковую разницу температур.Таким образом, коэффициент теплопередачи также зависит от направления теплового потока. В отличие от теплопроводности коэффициент теплопередачи не является материальной константой.
В чем разница между коэффициентом теплопередачи локальной конвекции и средним коэффициентом?
В чем разница между коэффициентом теплопередачи локальной конвекции и средним коэффициентом? Какие у них подразделения? Средний коэффициент теплопередачи — это среднее значение по поверхности. 1/3 = 1.В 59 раз выше исходного значения, т. Е. На 59% больше. Обратите внимание, что эти пропорции применимы только к полностью турбулентному потоку.
Почему в теплообменнике наблюдается перепад давления?
Падение давления на межтрубном пространстве Очень часто используются перегородки на межтрубном пространстве кожухотрубного теплообменника. Они заставляют жидкость со стороны кожуха проходить по трубам. Это вызывает условия «поперечного потока» и способствует общей теплопередаче. Например, со стороны кожуха обычно помещают более вязкую жидкость.
В чем причина высокого коэффициента конвективной теплоотдачи при капельной конденсации?
Капельная конденсация происходит, когда пар конденсируется на поверхности, не смачиваемой конденсатом. Для паров неметаллов капельная конденсация дает гораздо более высокие коэффициенты теплопередачи, чем те, которые наблюдаются при пленочной конденсации.
В каком режиме теплопередачи обычно выше коэффициент конвективной теплопередачи?
принудительная конвекция
Почему коэффициент теплопередачи при принудительной конвекции больше, чем при свободной конвекции?
Механизм принудительной конвекции Движение жидкости увеличивает теплопередачу (чем выше скорость, тем выше скорость теплопередачи).Коэффициент конвективной теплопередачи h сильно зависит от свойств жидкости и шероховатости твердой поверхности, а также от типа потока жидкости (ламинарный или турбулентный).
Упрощенная формула для оценки коэффициента теплопередачи естественной конвекции на плоской пластине
Хотя сегодня в сообществе систем охлаждения электроники основное внимание уделяется расширению возможностей принудительного конвекционного охлаждения, многие приложения по-прежнему зависят от охлаждения естественной конвекцией.По сути, охлаждение с естественной конвекцией в сочетании с излучением возникает, когда в конструкции охлаждения не используется вентилятор для перемещения воздуха. Вместо этого движение воздуха вызывается разницей в плотности, возникающей из-за рассеивания тепла электронными компонентами. Очевидное преимущество естественной конвекции, или «свободной» конвекции, как ее иногда называют, заключается в том, что исключается необходимость в установке вентилятора. Конечно, недостатком, связанным с этим методом охлаждения, является более низкий коэффициент теплопередачи.
Для оценки температуры поверхности компонентов, установленных на плате или плате, мы иногда аппроксимируем поверхность как плоскую пластину. Затем мы можем использовать безразмерные корреляции естественной конвекции для оценки коэффициента теплопередачи естественной конвекции [1]. Эти соотношения принимают вид
где
|
Значение константы C и показателя степени n будет зависеть от ориентации нагретой поверхности, как указано в таблице 1.
Таблица 1. Значение константы C и экспоненты n
|
Теплофизические свойства воздуха для использования в уравнениях 1 и 2 можно найти в любом учебнике по основам теплопередачи [2]. Используемые значения свойств воздуха должны соответствовать средней температуре пленки, которая определяется как среднее значение температуры поверхности и температуры наружного воздуха вдали от пластины.
Проблема использования этих корреляций заключается в том, что мы обычно имеем представление о рассеиваемой мощности и хотим вычислить температуру поверхности, чтобы мы могли оценить внутреннюю температуру некоторых компонентов.Поскольку мы не знаем температуру поверхности априори, мы должны угадать температуру, чтобы получить свойства воздуха, и T, чтобы использовать в корреляциях для вычисления h. К счастью, существует упрощенная формула для воздуха, которая дает коэффициент теплопередачи для естественного конвекция воздуха над плоской пластиной [1]. Эта формула имеет вид
Хотя эта формула также зависит от температуры поверхности, T с , если мы объединим ее с уравнением скорости Ньютона,
После небольшой алгебраической обработки мы можем получить выражение для T s как функцию рассеивания тепла q с поверхности пластины
На рисунке 1 показано сравнение значения естественной конвекции h для квадратной пластины диаметром 100 мм, рассчитанной с использованием безразмерного уравнения 2, с упрощенным уравнением размеров 3.Эти результаты показывают, что упрощенная формула занижает значение h на 3–6% для вертикальной пластины и горизонтальной пластины с нагретой стороной вверх. Для случая горизонтальной пластины с нагретой стороной вниз упрощенная формула занижает h на 13–15%.
Рисунок 1. Коэффициент теплопередачи в зависимости от температуры поверхности. Представленные здесь уравнения действительны только для ламинарной естественной конвекции. В большинстве приложений электронного охлаждения маловероятно, что будет встречаться турбулентная естественная конвекция.Следует также отметить, что как безразмерное уравнение, так и упрощенное размерное уравнение справедливы только в том случае, если поблизости нет поверхностей, которые препятствовали бы развитию пограничного слоя естественной конвекции. Влияние близлежащих поверхностей на естественную конвекцию теплопередачи — тема будущих колонн.
Ссылки
1. МакАдамс, WH, Теплопередача, 3-е изд., Макгроу-Хилл, Нью-Йорк, Нью-Йорк, 1954.
2. Инкропера, Ф.П., и Девитт, Д.П., Основы тепломассообмена, Джон Уайли and Sons, Нью-Йорк, Нью-Йорк, 1985.
Исследование коэффициента теплопередачи естественной конвекции на удлиненных вертикальных опорных плитах
Энергетика и энергетика, 2011, 3, 174-180
doi: 10.4236 / epe.2011.32022 Опубликовано в Интернете в мае 2011 г. (http: // www. SciRP.org/journal/epe)
Авторские права © 2011 SciRes. EPE
Исследование теплопередачи естественной конвекции
Коэффициент на удлиненных вертикальных опорных плитах
Махди Фахиминия1, Мохаммад Махди Насериан2, Хамид Реза Гошайеши1, Давуд Маджидиан3
1 Отделение, кафедра машиностроения, Меша, Иран
2 Клуб молодых исследователей, Мешхедский филиал, Исламский университет Азад, Мешхед, Иран
3 Кафедра системной инженерии, Политехнический институт Вирджинии и Государственный университет, США
Эл. Почта: MFahiminia @ Gmx.com, [email protected], [email protected], [email protected]
Поступило 21 декабря 2010 г .; отредактировано 8 апреля 2011 г .; принято 15 апреля 2011 г.
Реферат
В данном исследовании был проведен вычислительный анализ ламинарной естественной конвекции на вертикальных поверхностях. Естественная конвекция наблюдается, когда градиенты плотности присутствуют в жидкости, на которую действует гравитационное поле
. Нашим примером этого явления является нагретая вертикальная пластина, подверженная воздействию воздуха, который на расстоянии
от пластины неподвижен.Моделирование CFD выполняется с использованием программного обеспечения Fluent. Управляющие уравнения
решаются с использованием подхода конечных объемов. Связь между скоростью и давлением осуществляется с помощью алгоритма
SIMPLE. Полученная система дискретизированных линейных алгебраических уравнений решается с помощью неявной схемы с чередованием направлений. Затем на поверхность
разными способами наносится конфигурация из ребер прямоугольной формы и изучается коэффициент теплопередачи естественной конвекции на этих поверхностях без уклона, и, наконец, выполняется оптимизация
.
Ключевые слова: естественная конвекция, вертикальные поверхности, простой алгоритм, прямоугольные ребра
1. Введение
В этом документе естественная конвекция рассматривается как результат движения жидкости
, вызванный градиентом плотности
. Радиатор, который используется для обогрева дома —
— пример практического оборудования для естественной конвекции.
Движение жидкости, будь то газ или жидкость, в естественной
конвекции вызывается выталкивающей силой из-за уменьшения плотности
у поверхностей в процессе нагрева.Когда внешняя сила
, такая как сила тяжести, не влияет на жидкость
, силы плавучести не будет, и механизм
будет проводящим. Но сила тяжести — не единственная сила
, вызывающая естественную конвекцию. Когда жидкость находится во вращающейся машине
, на нее действует центробежная сила
, и если одна или несколько поверхностей с температурой более или менее
, чем у жидкости, соприкасаются с жидкостью
, будут наблюдаться естественные конвекционные потоки.Жидкость
, которая примыкает к вертикальной поверхности с постоянной температурой
, температура жидкости меньше, чем температура поверхности
, образует скоростной пограничный слой.
Профиль скорости в этом пограничном слое
полностью отличается от профиля скорости при принудительной конвекции.
Скорость на стене равна нулю из-за отсутствия скольжения.
Затем скорость увеличивается и достигает своего максимума, и
, наконец, достигает нуля на внешней границе пограничного слоя скорости
.Поскольку фактором, вызывающим естественную конвекцию
, является температурный градиент, также появляется граничный слой нагрева —
. Температурный профиль также
имеет такое же значение, что и температура стенки из-за отсутствия
частиц, скользящих по стенке, а температура частиц
понижается по мере приближения к внешней границе температурного пограничного слоя
и он достиг бы температуры далекой жидкости.


 Почему? Это объясняется недостаточной теплопроводностью воды для передачи тепла в нижнюю часть пробирки.
Почему? Это объясняется недостаточной теплопроводностью воды для передачи тепла в нижнюю часть пробирки. Жидкость начинает понемногу окрашиваться, но это происходит благодаря явлению диффузии (т. е. из-за непрерывного хаотичного теплового движения частиц вещества), а конвективные потоки пока не будут наблюдаться. Затем располагаем зажженную свечу под одним из колен трубки, как это показано на рисунке 3.
Жидкость начинает понемногу окрашиваться, но это происходит благодаря явлению диффузии (т. е. из-за непрерывного хаотичного теплового движения частиц вещества), а конвективные потоки пока не будут наблюдаться. Затем располагаем зажженную свечу под одним из колен трубки, как это показано на рисунке 3.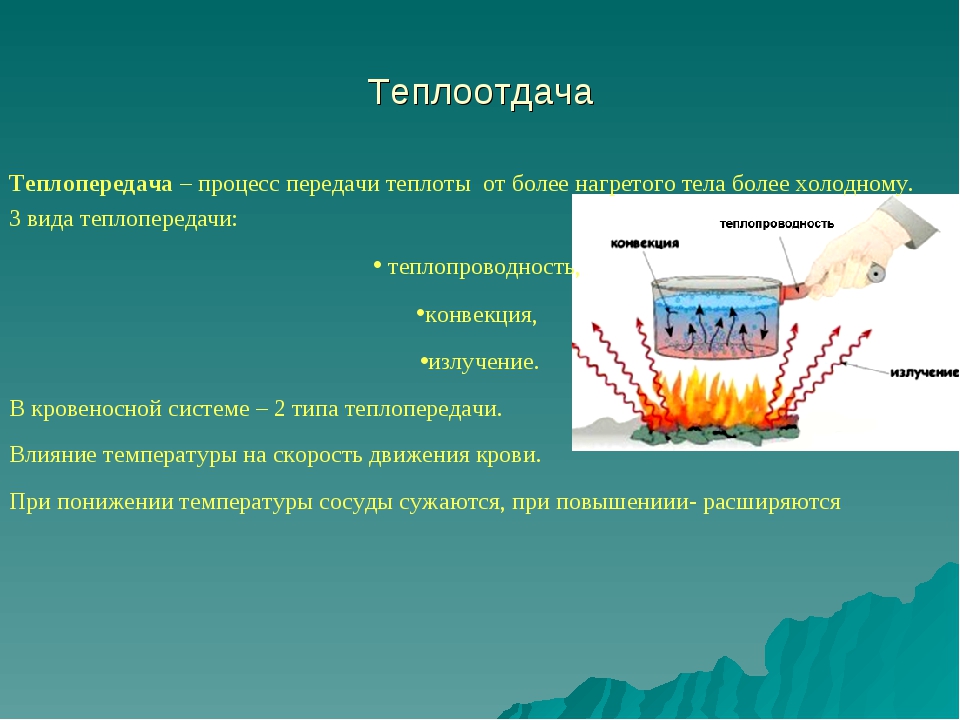 Таким образом, мы имеем возможность наблюдать циркуляцию конвективных потоков в жидкости.
Таким образом, мы имеем возможность наблюдать циркуляцию конвективных потоков в жидкости.



 Обустраивается в мультифункциональных моделях, типа Electrolux EOB55351AX. Тепло в таких духовках присутствует равномерно распределяется за счет вентилятора. Иногда он комбинируется с электрическими тэнами для полноценного пропекания.
Обустраивается в мультифункциональных моделях, типа Electrolux EOB55351AX. Тепло в таких духовках присутствует равномерно распределяется за счет вентилятора. Иногда он комбинируется с электрическими тэнами для полноценного пропекания. In на самом деле, когда плотность изменяется с температурой, плавучесть возникает в нормальном потоке, и интересно знать, когда ею можно пренебречь, а когда нужно учитывать. Это соображение осложняется большим количеством влияний parameters. In помимо числа Рейнольдса и числа Прандтля, число глашофа также имеет важное значение.
In на самом деле, когда плотность изменяется с температурой, плавучесть возникает в нормальном потоке, и интересно знать, когда ею можно пренебречь, а когда нужно учитывать. Это соображение осложняется большим количеством влияний parameters. In помимо числа Рейнольдса и числа Прандтля, число глашофа также имеет важное значение. Людмила Фирмаль
Людмила Фирмаль охлаждающие каналы расположены по оси, параллельной оси вращения, длиной 5,08 см, расстоянием от оси 38,1 см.
охлаждающие каналы расположены по оси, параллельной оси вращения, длиной 5,08 см, расстоянием от оси 38,1 см. Людмила Фирмаль
Людмила Фирмаль
