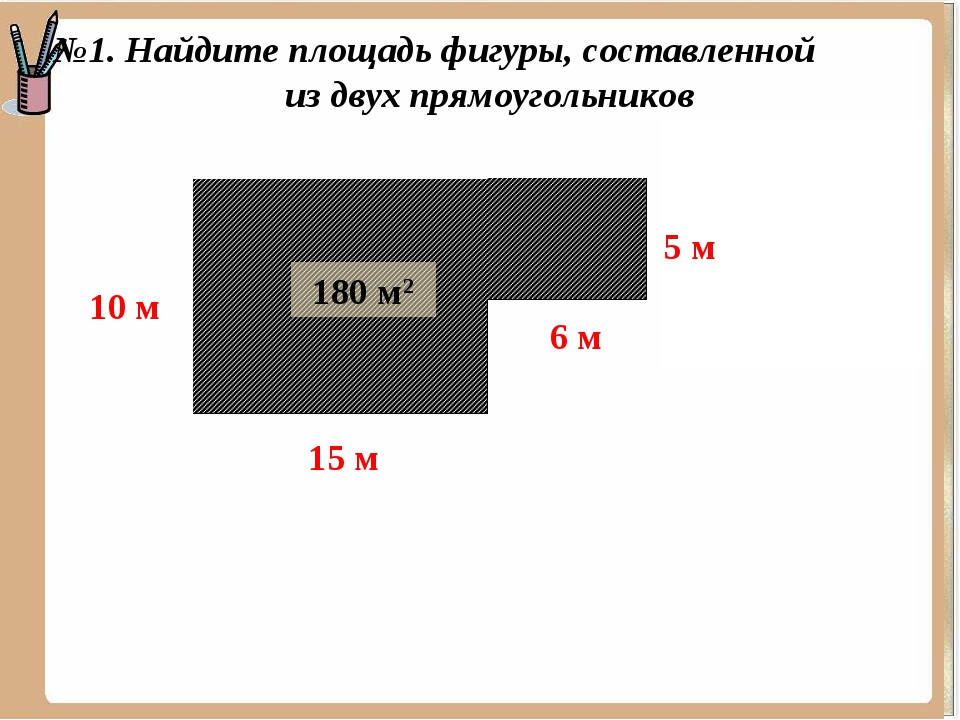
Площадь прямоугольника — как ее найти по основной формуле, а также через диагональ и периметр
Обновлено 22 июля 2021 Просмотров: 173 413 Автор: Дмитрий Петров- Что такое площадь
- Как найти площадь прямоугольника
- Формула площади через периметр
- Площадь прямоугольника через диагональ
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.
Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:
А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.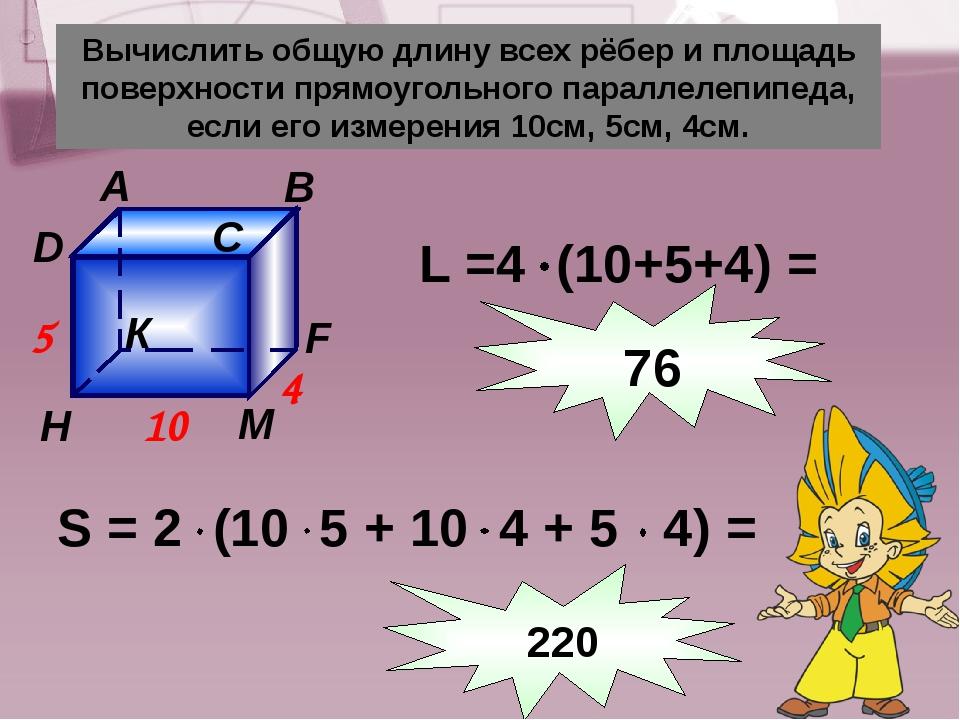
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».
Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
Возьмем, к примеру, такой прямоугольник:
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
И тогда обратные расчеты выглядят вот так:
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле. - Ну и второй вариант – воспользоваться сразу готовой формулой:
Площадь прямоугольника через диагональ
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
Второй вариант – опять же сразу прибегнуть к готовой формуле:
Если известны длина диагоналей и угол между ними.
В этом случае стоит воспользоваться вот такой формулой:
Вот и все, что нужно знать о вычислении площади прямоугольников.
youtube.com/embed/xV0EBP2hyrM?start=11″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings. DRAG_TEXT}}
DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
 selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}Как найти площадь двух квадратов. Что такое площадь квадрата? Формулы площади, примеры расчетов
Формула площади необходима для определения площадь фигуры, которая является вещественнозначной функцией, определённой на некотором классе фигур евклидовой плоскости и удовлетворяющая 4м условиям:
- Положительность — Площадь не может быть меньше нуля;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения 2х фигур без общих внутренних точек равна сумме площадей этих фигур.
| Геометрическая фигура | Формула | Чертеж |
|---|---|---|
Результат сложения расстояний между серединами противоположных сторон выпуклого четырехугольника будут равна его полупериметру. | ||
Сектор круга. Площадь сектора круга равна произведению его дуги на половину радиуса. | ||
Сегмент круга. Чтобы получить площадь сегмента ASB, достаточно из площади сектора AOB вычесть площадь треугольника AOB. | S = 1 / 2 R(s — AС) | |
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. | ||
Эллипс . Еще один вариант как вычислить площадь эллипса — через два его радиуса. | ||
Треугольник. Формула площади круга через его радиус и диаметр. | ||
Квадрат . Через его сторону. Площадь квадрата равна квадрату длины его стороны. | ||
Квадрат. Через его диагонали . Площадь квадрата равна половине квадрата длины его диагонали. | ||
Правильный многоугольник . Для определения площади правильного многоугольника необходимо разбить его на равные треугольники, которые бы имели общую вершину в центре вписанной окружности. | S= r·p = 1/2 r·n·a |
Кто-то из нас математику в школе просто прогуливал, кто-то проболел, а кто-то подзабыл за давностью школьных лет, но так или иначе, рано или поздно возникает вопрос: «Как найти площадь квадрата?»
Самая основная формула того, как найти площадь квадрата:
S=a 2 , где:
- S — площадь квадрата,
- а — сторона квадрата.

Так как у квадрата все стороны равны, то площадь квадрата — это сторона в квадрате. Например, нам известно, что длина стороны квадрата — 4 см. Тогда по формуле S=a 2 получится: S=4 2 =16 (см 2).
Ещё один способ нахождения площади квадрата — по периметру. Периметр квадрата (Р) равен сумме всех сторон квадрата, а так как у квадрата все стороны равны, то имеет следующую формулу:
Р=4а , где:
- Р — периметр квадрата,
- а — сторона квадрата.
Таким образом, если нам известен периметр квадрата, мы можем вычислить его площадь по следующей формуле:
Разделив периметр на 4, мы получим длину одной стороны квадрата, после чего по первой формуле легко вычислить площадь.
Также можно найти площадь квадрата, если известна длина его диагонали. Особенности квадрата, как геометрической фигуры таковы, что его диагонали (отрезок, проведённые между несмежными вершинами квадрата) делят квадрат на два прямоугольных и равнобедренных треугольника. Прямоугольный треугольник — это такой треугольник, в составе которого есть прямой угол, а нам известно, что у квадрата все углы прямые. Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Диагонали квадрата являются одновременно и биссектрисами его углов. Биссектриса — это луч, которая делит угол пополам.
Прямоугольный треугольник — это такой треугольник, в составе которого есть прямой угол, а нам известно, что у квадрата все углы прямые. Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Диагонали квадрата являются одновременно и биссектрисами его углов. Биссектриса — это луч, которая делит угол пополам.
По теореме Пифагора известно, что квадрат гипотенузы равен сумме квадратов катетов:
с 2 = b 2 + a 2
Но так как у нас катеты равны, то формула будет иметь следующий вид:
с 2 = а 2 + а 2 = 2а 2
В нашем случае гипотенуза — это диагональ квадрата (с = d), а катеты — сторона (b,е = a). Имеем:
Из вышеприведённой формулы можно вывести формулу нахождения катета (стороны квадрата):
Подставляем данное значение в первую формулу:
Сокращаем значения корня и второй степени и получаем формулу:
Например, если диагональ равна 8 см., то площадь квадрата равна:
S=8 2 /2 = 32 (см.).
Ещё одна формула нахождения площади квадрата — по радиусу вписанной (r) и описанной (R) окружности.
Вписанная окружность — это окружность, которая касается середины каждой стороны квадрата и имеет радиус, равный половине середины стороны:
Описанная окружность – это такая окружность, которая касается вершины каждого угла квадрата:
Таким образом, для нахождения площади квадрата при помощи радиуса вписанной окружности получаем следующую формулу:
S=(2r) 2 =2 2 *r 2 =4r 2
Например, если радиус вписанной окружности 3 см., то
S=4*3 2 =4*9=36 (см.).
Для нахождения площади квадрата при помощи радиуса описанной окружности получаем такую формулу:
S=d 2 /2=2R 2 /2=(2 2 *R 2)/2=2R 2
Таким образом, если радиус описанной окружности равен 4, то по формуле:
S=2*4 2 =2*16=32 (см).
Вот все способы того, как найти площадь квадрата, формулы вы также имели возможность вывести сами. Успешных Вам решений!
Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Площадь квадрата и как ее найти
Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.
Как найти периметр квадратаПериметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.
Пример:
- сторона квадрата = 5, следовательно, P = 4*5 = 20
- сторона квадрата = 3, следовательно, Р = 4*3 = 12
Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.
При решении нужны формулы, которые представлены ранее.
Например: как найти периметр квадрата, если известна площадь, равная 144?
Шаги решения:
- Выясняем длину одной стороны: а = √144 = 12
- Находим периметр: Р = 4*12 = 48.
Нахождение периметра вписанного квадрата
Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Алгоритм решения:
- так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
- затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
- делим уравнение на 2: (a 2 ) = 2(r) 2 ;
- извлекаем корень: a = √(2r).
В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).
- Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:
Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a
2
) = 10
2
, то есть 2a
2
= 100. Делим полученное на два и в результате: a
2
= 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Рассмотрим еще один вопрос
Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?
Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см
2
, найдите его периметр.
Шаги решения:
- Находим сторону квадрата: а = √25 = 5.
- Находим сам периметр: Р = 4*а = 4*5 = 20.
Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.
Нужно в вышеуказанную формулу подставить его стороны. Но они равны, получается, чтобы найти площадь правильного прямоугольника нужно возвести в квадрат его сторону. S = (a) во второй степени.
Теперь по формуле площади квадрата можно найти его сторону, зная численное значение площади. Для этого нужно решить уравнение второй степени: S=(a) во второй степени. Находится сторона «а» путем извлечения из под корня площади фигуры: а = корень квадратный из (S). Пример: нужно найти сторону квадрата, если его площадь составляет шестьдесят четыре квадратных сантиметров. Решение: если 64=(а) в кавдрате, то «а» равно корень из шестидесяти четырех. Получается восемь. Ответ: восемь квадратных сантиметров.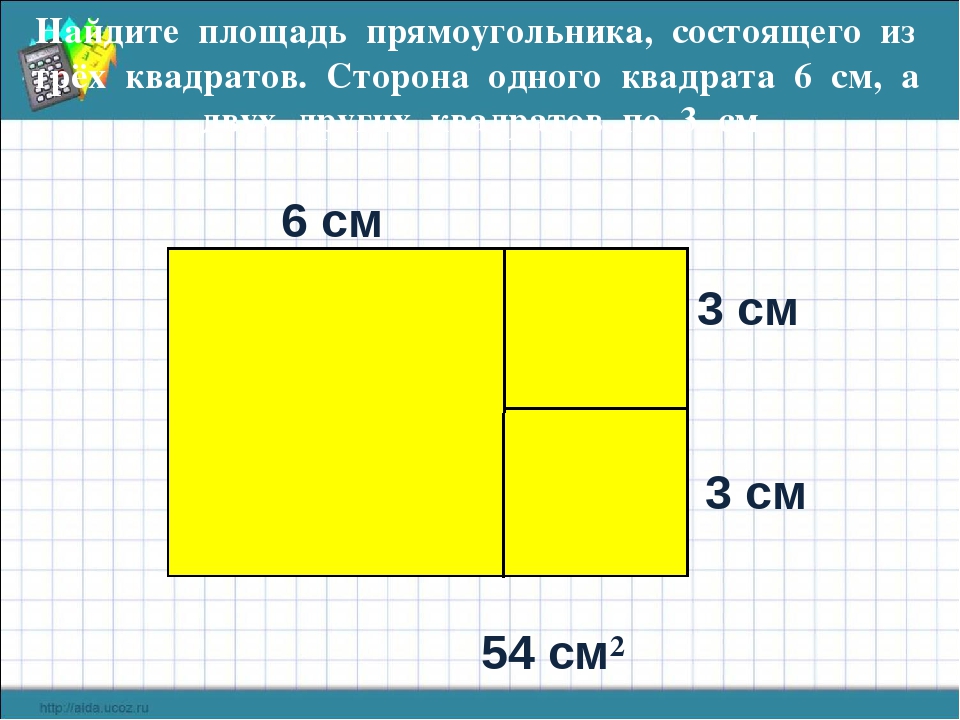
Если решение квадратного корня выходит за рамки таблицы квадратов и ответ не получается целым, спасет микрокалькулятор. Даже на самой простой машинке можно найти значение из под корня второй степени. Для этого наберите следующий набор кнопок: «число», которое выражает подкоренное выражение и «знак корня». Ответ на экране и будет подкоренным значением.
Куб представляет собой частный случай параллелепипеда, в котором каждая из граней образована правильным многоугольником — квадратом. Всего куб обладает шестью гранями. Вычислить площадь не представляет затруднений.
Инструкция
Теперь, зная площадь одной из грани квадрата, можно узнать площадь всей поверхности куба. Это можно осуществить, если модифицировать формулу, указанную выше:
S = 6*a²
Иначе говоря, зная, что таких квадратов (граней) у куба аж шесть штук, то площадь поверхности куба составляет одной из граней куба.
Для наглядности и удобства можно привести пример:
Допустим, дан куб, у которого длина ребра равна 6 см, требуется найти площадь поверхности данного куба. Первоначально потребуется найти площадь грани:
Первоначально потребуется найти площадь грани:
S = 6*6 = 36 см²
Таким образом, узнав площадь грани, можно найти и всю площади поверхности куба:
S = 36*6 = 216 см²
Ответ: площадь поверхности куба с ребром, равным 6 см, составляет 216 см²
Обратите внимание
Куб является частным случаем не только параллелепипеда, но и призмы.
Параллелепипедом называется призма, у которого основанием является параллелограмм. Особенностью параллелепипеда является то, что 4 из 6 его граней — прямоугольники.
Призмой считается многогранник, в основании которого находятся равные многоугольники. Одной из главных особенностей призмы можно назвать то, что боковые грани ее является параллелограммами.
Помимо куба, существуют и иные виды многогранников: пирамиды, призмы, параллелепипеды и т.д., каждому из них соответствуют различные способы нахождения площадей их поверхностей.
Полезный совет
Если дан не куб, а иной правильный многогранник, то в любом случае, площадь его поверхности будет находиться аналогично. Это означает, что площадь поверхности правильного многогранника находится путем суммирования всех площадей его граней — правильных многоугольников.
Это означает, что площадь поверхности правильного многогранника находится путем суммирования всех площадей его граней — правильных многоугольников.
Кубом называют объемную геометрическую фигуру с восемью ребрами, двенадцатью вершинами и шестью гранями. От параллелепипеда, имеющего такие же параметры, ее отличают обязательное равенство длин всех ребер и прямые углы в вершинах каждой грани. Простота этой фигуры делает несложным вычисление общей площади поверхности всех ее граней.
Инструкция
Если известна длина куба (a), то вы можете использовать наиболее распространенный из всех возможных вариантов формулы вычисления площади (S). По определению каждая грань этой фигуры имеет квадрата, а его площадь равна длине грани, возведенной во вторую степень. Так как всего таких граней у куба шесть, то это число надо увеличить именно во столько раз: S = 6*a².
Если длина ребра неизвестна, но дан объем (V) пространства, ограничиваемого сторонами куба, то площадь (S) тоже можно . Так как известная из условий величина для этой фигуры находится возведением длины ребра в третью степень, то длину стороны каждой грани можно определить, если извлечь кубический корень из этого параметра. Подставьте это выражение в равенство из предыдущего шага и вы получите такую формулу: S = 6*(³√V)².
Так как известная из условий величина для этой фигуры находится возведением длины ребра в третью степень, то длину стороны каждой грани можно определить, если извлечь кубический корень из этого параметра. Подставьте это выражение в равенство из предыдущего шага и вы получите такую формулу: S = 6*(³√V)².
Если известна длина диагонали куба (L), то через нее тоже можно выразить длину одной грани, а значит и рассчитать площадь поверхности гексаэдра. Диагональ находится умножением длины грани на квадратный корень из тройки — выразите из этой формулы размер одной стороны квадрата и подставьте полученное значение во все то же равенство из первого шага: S = 6*(L/√3)² = 2*L².
Если известен радиус описанной около куба сферы (R), то формулу вычисления площади поверхности можно вывести из полученного на предыдущем шагу выражения. Так как любая из диагоналей куба совпадает с диаметром такой сферы, а диаметр — это удвоенный радиус, то вам надо трансформировать формулу к такому виду: S = 2*(2*R)² = 8*R².
Еще проще получить формулу вычисления площади поверхности (S) гексаэдра, если известен радиус (r) не описанной, а вписанной в эту фигуру сферы. Ее диаметр (удвоенный радиус) равен длине ребра куба. Подставьте это значение в формулу из первого шага и получите такое равенство: S = 6*(2*r)² = 24*r².
Грань куба представляет собой квадрат, диагональ которого делит его на два равных прямоугольных треугольника, являясь их гипотенузой. Именно поэтому все используемые здесь формулы в той или иной степени основаны на применении теоремы Пифагора. В зависимости от имеющихся данных вы сможете найти площадь грани (квадрата) куба несколькими различными способами.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Как вычислить размеры квартиры, зная площадь? На примере планировки студии
В настоящее время многие жители России приобретают недвижимость в новостройках, причём ещё на этапе строительства. Однако зачастую застройщики не прилагают к договору планировку будущей квартиры с точными размерами. Видимо чтобы потом не было претензий по неточному соответствию результата планам.
Однако зачастую застройщики не прилагают к договору планировку будущей квартиры с точными размерами. Видимо чтобы потом не было претензий по неточному соответствию результата планам.
Однако планировку с площадями помещений застройщик чаще всего предоставляет, такие планировки выложены обычно прямо на официальном сайте. Покупатель сможет узнать точные размеры квартиры только при приёмке, однако многие хотят начать заранее планировать своё будущее жизненное пространство. Поэтому было бы нелишним заранее вычислить размеры исходя из площадей комнат и квартиры в целом. Конечно же погрешность в десяток сантиметров весьма ощутима, и по вычисленным значениям нельзя заказывать мебель. Зато это позволит примерно прикинуть, куда и какая мебель сможет поместиться.
В статье расчёты будем производить на основе чертежа-планировки квартиры-студии в одном из проектов строительной компании ПИК.
Пример планировки с площадью, но без размеров
Приведём пример того, как найти размеры, зная только общую площадь квартиры. Точность метода напрямую зависит от точности соблюдения масштаба имеющейся у вас планировки, указанных площадей комнат и ваших измерений.
Точность метода напрямую зависит от точности соблюдения масштаба имеющейся у вас планировки, указанных площадей комнат и ваших измерений.
1. Найдём общую площадь квартиры в квадратных метрах. Скорее всего эта цифра указана в договоре или подписана на планировке. Общая площадь находится как сумма площадей всех комнат. В приведенном примере площади всех помещений подписаны прямо на планировке. Остаётся их только сложить. Таким образом, получим, что реальная площадь (So) = 3,9 + 4,1 + 6,3 + 14,2 = 28,5 квадратных метров.
2. Далее найдём общую площадь квартиры в условных единицах. Не важно, что это будут за единицы измерения. Например, если вы будете измерять распечатанный чертеж с помощью линейки, то у вас будут миллиметры или сантиметры. Если же замеры будут производиться на компьютере, то у вас будут пиксели.
Планировка у нас скачена с официального сайта компании-застройщика, поэтому откроем изображение планировки квартиры в графическом редакторе, например, Adobe Photoshop. Принцип подсчёта тот же самый — следует померить площадь каждого помещения квартиры и сложить полученные значения.
Принцип подсчёта тот же самый — следует померить площадь каждого помещения квартиры и сложить полученные значения.
Планировка с измеренными размерами
В примере всё предельно просто — квартира-студия представляет собой прямоугольник, поэтому можно просто перемножить его стороны 583 х 1494 пикселя. Итого получим 871002 квадратных пикселя — площадь квартиры по схеме квартиры (Su).
Для большей точности конечно же следовало бы также вычесть площадь стен ванной комнаты.
3. Следующий шаг в алгоритме поиска размеров квартиры — найти коэффициент масштаба. То есть во сколько раз имеющаяся у вас планировка меньшем, чем реальная квартира. Для этого потребуется решить простейшее уравнение, которое можно записать так: Su * k * k = Sр. Заменив исходную площадь на длину и ширину, получим: Wu * k * Hu * k = Su, где Wu, Hu и Su — ширина, длина и площадь по чертежу (исходные). Таким образом, коэффициент масштаба будет равен квадратному корню из отношения реальной площади к площади, измеренной по планировке.
Таким образом, коэффициент масштаба будет равен квадратному корню из отношения реальной площади к площади, измеренной по планировке.
k = 0,00572022
4. Остаётся на основе найденного коэффициента найти реальные ширину и длину. Для этого умножим измеренные значения на найденный коэффициент:
Wр = 583 * k = 3,335 м
Hр = 1494 * k = 8,546 м
Следует отметить, что у вас может быть более сложная планировка, поэтому вычислить суммарную площадь квартиры не всегда может быть так просто. Поэтому можно сделать всё тоже самое только для одной конкретной комнаты и на её основе найти масштаб. Особенно хорошо будет, если форма у комнаты будет обычной прямоугольной формы, это позволит выполнить вычисления с минимальной погрешность.
5. Далее исходя из процентного соотношения размеров стен друг к другу находим реальные размеры стен. Например, в представленной выше планировке, стена от окна до туалета занимает 69% от общей длины, которая составляет 8,546 м, поэтому этот участок будет равен 0,695 * 8,546 м = 5,94 метра.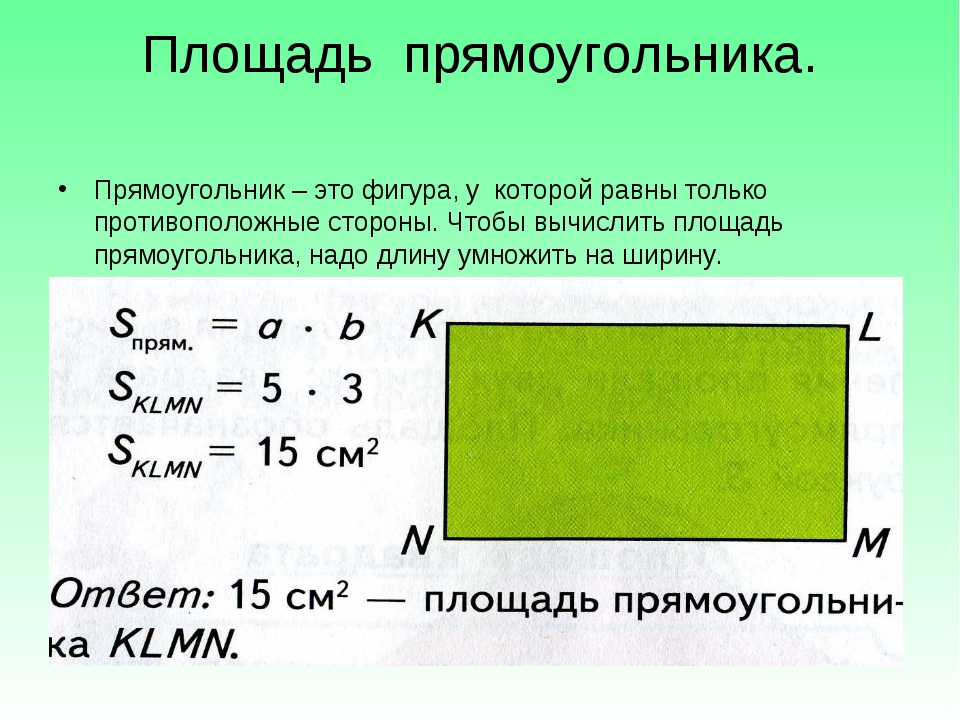 Таким же образом, можно узнать размеры всех других стен в квартире.
Таким же образом, можно узнать размеры всех других стен в квартире.
Как видно, вычислить размеры квартиры, зная только её площадь, не составит никакого труда — нужно лишь выполнить пару арифметических действий.
В общую площадь входят площади всех помещений квартиры
291.5.3. фізичні особи — підприємці, які надають в оренду земельні ділянки, загальна площа яких перевищує 0,2 гектара, житлові приміщення, та/або їхчастини , житлова(нов.ред) (загальна) площа яких перевищує 100 квадратних метрів, нежитлові приміщення (споруди, будівлі) та/або їх частини, загальна площа яких перевищує 300 квадратних метрів;
СПРАВКА
В общую площадь входят площади всех помещений квартиры, встроенных шкафов, а также площади лоджий, балконов, веранд, террас и холодных кладовых. Для последних используются понижающие коэффициенты: площадь лоджий умножают на 0,5; балконов, террас – на 0,3.Показатель «общая площадь жилья» используется для расчета платы за содержание и ремонт жилья (техническое обслуживание).
Полезная площадь. Для определения платы за отопление в расчете на 1 кв. м жилья площадь определяется как суммарная жилых комнат и подсобных помещений без учета лоджий, балконов, веранд, террас и холодных кладовых, тамбуров.
Жилая площадь квартиры — это сумма площадей жилых помещений.
Площадь помещений определяется в результате их измерения между отделанными поверхностями стен и перегородок на уровне пола без учета плинтусов.
Жилая площадь – та, в которой люди живут: спальня, гостиная, детская. Площадь квартиры – это все, что отапливается. Общая площадь вбирает в себя и холодные кладовые, и балконы (лоджии), и встроенные шкафы. Площадь лоджии, балкона, веранды обычно включают в общую площадь с понижающим коэффициентом (лоджия – с коэффициентом 0,5). Единственный спорный вопрос — веранда, так как ее отличия от лоджии незначительны (самое существенное из них то, что веранда застеклена). Этим спорным моментом и пользуются недобросовестные застройщики.
В чем разница между видами площади квартиры?
Жилая площадь квартиры определяется как сумма площадей жилых комнат.
Площадь квартиры определяется как сумма площадей жилых комнат и подсобных помещений (к ним относятся кухни, коридоры, ванные, санузлы, встроенные шкафы, кладовые, а также площадь, занятая внутриквартирной лестницей) без учета лоджий, балконов, веранд, террас, холодных кладовых и тамбуров. «Применявшееся ранее в официальном статистическом учете жилищного фонда понятие «общая площадь» равнозначно понятию «площадь квартиры».
Общая площадь квартиры определяется как сумма площадей ее помещений, встроенных шкафов, а также площадей лоджий, балконов, веранд, террас и холодных кладовых, подсчитываемых со следующими понижающими коэффициентами: для лоджий — 0,5, для балконов и террас — 0,3, для веранд и холодных кладовых — 1,0.(Определения даны в СНиП 31.01.2003)
Для чего нужны три разных учета площади одной и той же квартиры?
Показатели общей площади квартиры используются для целей государственного статистического наблюдения объемов жилищного строительства. Показатели площади квартиры используются для целей официального статистического учета жилищного фонда в Российской Федерации, оплаты жилья и коммунальных услуг, определения социальной нормы жилья и иных целей.
Показатели площади квартиры используются для целей официального статистического учета жилищного фонда в Российской Федерации, оплаты жилья и коммунальных услуг, определения социальной нормы жилья и иных целей.
Для чего нужно знать обычному человеку о разнице между жилой площадью, общей площадью и площадью квартиры?
Описание квартиры, которое содержится в договоре о купле-продаже квартиры, говорит о комфортабельности жилья и дает информацию о том, как складывается его цена.Хотя каждый застройщик по-своему формирует договор о долевом строительстве, он должен в нем четко указать цену квадратного метра, а также из чего она складывается, в том числе — включается ли в оплату площадь лоджии (или балкона, или веранды) и на каких условиях. Желательно, чтобы клиент обратил на это внимание, спросил, что входит в понятие общей площади, сколько метров жилой площади оплачиваются, чтобы в дальнейшем, когда озвучат полную стоимость квартиры, знать, за что конкретно он отдает свои деньги. Потому что когда человек получит свидетельство, в нем будет указана общая площадь квартиры без учета лоджий и балконов.
Потому что когда человек получит свидетельство, в нем будет указана общая площадь квартиры без учета лоджий и балконов.
«В соответствии с данными в СНиП 2.08.01-89 «Жилые здания» (приложение 1) определениями понятий «балкон», «лоджия» и «веранда» и сложившейся практикой строительства, термины «остекленная лоджия», «остекленный балкон» и «веранда» имеют следующие значения: — верандой является встроенное или пристроенное к индивидуальному жилому дому остекленное неотапливаемое помещение, не взаимоувязанное с освещением примыкающего к ней помещения и не имеющее ограничения по глубине; — лоджией (остекленной или не остекленной) является помещение, встроенное в жилое многоквартирное здание и имеющее ограниченную глубину, взаимоувязанную с освещением помещения, к которому она примыкает; — остекленный балкон, как и лоджия, является частью многоэтажного жилого дома и имеет ограниченную глубину, взаимоувязанную с освещением помещения, к которому он примыкает. Исходя из данных выше определений, ни остекленная лоджии, ни остекленный балкон не могут являться верандой».
Калькулятор площади
Квадратная пирамида в форме
h = высота
s = наклонная высота
a = длина стороны
e = длина боковой кромки
г = а / 2
В = объем
S tot = общая площадь поверхности
S lat = площадь боковой поверхности
S bot = площадь нижней поверхности
Рассчитывайте больше с
Калькулятор пирамид
Использование калькулятора
Онлайн-калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усеченную вершину, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферический колпачок и треугольную призму
Единицы: Обратите внимание, что единицы показаны для удобства, но не влияют на вычисления. Единицы измерения указывают порядок результатов, например футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к V в мм 3 и S в мм 2 .
Единицы измерения указывают порядок результатов, например футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши вычисления приведут к V в мм 3 и S в мм 2 .
Ниже приведены стандартные формулы для расчета площади поверхности.
Формулы площади поверхности:
Площадь поверхности капсулы
- Объем = πr 2 ((4/3) r + a)
- Площадь поверхности = 2πr (2r + a)
Площадь поверхности круглого конуса
- Объем = (1/3) πr 2 ч
- Площадь боковой поверхности = πrs = πr√ (r 2 + h 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь
= L + B = πrs + πr 2 = πr (s + r) = πr (r + √ (r 2 + h 2 ))Площадь поверхности круглого цилиндра
- Объем = πr 2 ч
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь
= L + T + B = 2πrh + 2 (πr 2 ) = 2πr (h + r)Площадь поверхности конической усадки
- Объем = (1/3) πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π (r 1 + r 2 ) s = π (r 1 + r 2 ) √ ((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = πr 1 2
- Площадь базовой поверхности = πr 2 2
- Общая площадь
= π (r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π [r 1 2 + r 2 2 + (r 1 * r 2 ) * √ ((r 1 — r 2 ) 2 + h 2 )]Площадь поверхности куба
- Объем = a 3
- Площадь поверхности = 6a 2
Площадь поверхности полушария
- Объем = (2/3) πr 3
- Площадь изогнутой поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Площадь поверхности пирамиды
- Объем = (1/3) 2 ч
- Площадь боковой поверхности = a√ (a 2 + 4h 2 )
- Площадь базовой поверхности = 2
- Общая площадь
= L + B = a 2 + a√ (a 2 + 4h 2 ))
= a (a + √ (a 2 + 4h 2 ))Площадь поверхности прямоугольной призмы
- Объем =
л / ч.- Площадь поверхности = 2 (lw + lh + wh)
Площадь поверхности сферы
- Объем = (4/3) πr 3
- Площадь поверхности = 4πr 2
Площадь поверхности сферической крышки
- Объем = (1/3) πh 2 (3R — h)
- Площадь поверхности = 2πRh
Площадь поверхности треугольной призмы
Площадь верхней поверхности треугольной призмы по формуле
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {\ begin {align} (a + & b + c) (b + ca) \\ & \ times (c + ab) (a + bc ) \ конец {выровнено}} \]
Площадь нижней поверхности треугольной призмы по формуле
\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {\ begin {align} (a + & b + c) (b + ca) \\ & \ times (c + ab) (a + bc ) \ конец {выровнено}} \]
Площадь боковой поверхности треугольной призмы Формула
\ [A_ {lat} = h (a + b + c) \]Общая площадь поверхности треугольной призмы по формуле
\ [A_ {tot} = A_ {верх} + A_ {бот} + A_ {широта} \]
Как найти объем и площадь поверхности для 6 общих форм
Наш мир наполнен трехмерными объектами.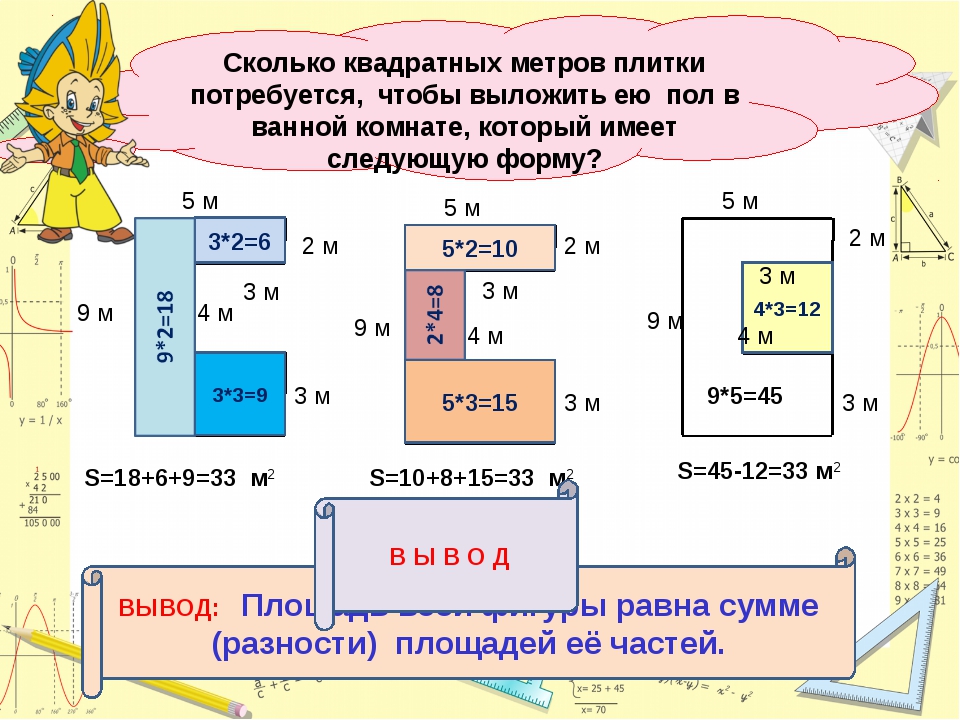 Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей базовой, верхней и боковых поверхностей (сторон) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Когда дело доходит до знания объема и площади поверхности этих объектов, вам необходимо знать два определения. Площадь поверхности — это площадь всех внешних поверхностей объекта. Общая площадь поверхности рассчитывается путем сложения всех площадей на поверхности: площадей базовой, верхней и боковых поверхностей (сторон) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Объем — это объем пространства, который занимает трехмерный объект. Также существуют разные формулы для разных трехмерных форм.Общий объем объекта измеряется в кубических единицах.
Общие формулы для объема и площади поверхности
У нас есть для вас шпаргалка — формулы объема и площади поверхности для обычных форм. Использовать его с умом!
Формулы площади поверхности
Площадь поверхности куба составляет 6s² , где s — длина стороны.
Площадь поверхности прямоугольной призмы составляет 2 (wl + hl + hw) , где w — ширина, h — высота, l — длина.
Площадь поверхности сферы составляет 4πr² , где r — радиус сферы.
Площадь поверхности цилиндра составляет 2πrh + 2πr² , где r — радиус цилиндра, а высота — высота.
Площадь поверхности конуса составляет πrs + πr² , где r — радиус конуса, а s — наклон.
Формулы объема
Объем куба s³ , где s — длина стороны.
Объем прямоугольной призмы равен по высоте , где w — ширина, h — высота, l — длина.
Объем сферы равен ( 4πr³ ) /3 , где r — радиус сферы.
Объем цилиндра составляет πr²h , где r — радиус цилиндра, а высота — высота.
Объем конуса составляет (πr²h) / 3 , где r — радиус конуса, а s — наклон.
Пример расчета объема и площади поверхности
Чтобы найти участки поверхности объектов с криволинейной поверхностью, таких как сфера, нет другого выбора, кроме как запомнить формулы объема и площади поверхности. Но что касается других объектов, мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, с пирамидой вы просто вычисляете площадь основания и добавляете ее к площади каждой стороны треугольника.
Но что касается других объектов, мы часто можем разбить их на другие узнаваемые многоугольники и формы, объем или площадь поверхности которых мы можем легко найти. Например, с пирамидой вы просто вычисляете площадь основания и добавляете ее к площади каждой стороны треугольника.
Давайте найдем площадь поверхности и объем квадратной пирамиды с длиной основания 6 дюймов и наклонной высотой 5 дюймов.
Площадь квадратной пирамиды
- Чтобы найти общую площадь поверхности, сначала исследуем площадь основания, которая представляет собой просто квадрат.Мы знаем, что площадь квадрата составляет b² , где b — длина стороны. В данном случае площадь поверхности составляет 6² или 36 квадратных дюймов.
- Затем мы смотрим на четыре стороны, которые представляют собой просто треугольники. Мы знаем, что площадь треугольника составляет всего (bh) / 2 , где b — основание, а h — высота. В этом случае основание треугольника совпадает с основанием пирамиды b.
 Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна:
Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна:
- Когда мы сложим четыре из этих треугольников с площадью квадратного основания, мы получим общую площадь поверхности b² + 4 (bs) / 2, или b² + 2bs для квадратной пирамиды.Подсчитывая числа, мы получаем:
Объем квадратной пирамиды
Объем пирамиды соответствует этой формуле объема:
Мы можем подставить наши значения для высоты и основания, чтобы получить:
Распознавание объема и площади поверхности
Опять же, площадь поверхности измеряет общую площадь внешних поверхностей объекта, а объем измеряет внутреннее пространство, которое занимает объект.
Вы найдете множество реальных случаев, когда расчет площади поверхности или объема будет полезен, например, количество воды, необходимое для наполнения бассейна (прямоугольная призма), или количество оберточной бумаги, необходимое для обертывания. свеча (цилиндр) или баскетбольный мяч (шар).Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
свеча (цилиндр) или баскетбольный мяч (шар).Но всегда есть формулы для самых распространенных форм. Хотя полезно пройтись по формулам, прежде чем вам понадобится их использовать, не думайте, что вам нужно запоминать их все! Просто добавьте этот список в закладки, когда он вам понадобится.
Дополнительные домашние задания по математике
Как найти площадь поверхности куба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Площадь цилиндра
Поскольку
цилиндр
тесно связан с
призма
, формулы для их
площади поверхности
относятся к.
Помните, что формулы для площади боковой поверхности призмы п час а общая площадь поверхности равна п час + 2 B . Поскольку основание цилиндра — окружность, подставим 2 π р за п и π р 2 за B где р — радиус основания цилиндра.
Итак, формула для площадь боковой поверхности цилиндра L . S . А . знак равно 2 π р час .
Пример 1:
Найдите площадь боковой поверхности цилиндра с радиусом основания
3
дюймов и высотой
9
дюймы.
L . S . А . знак равно 2 π ( 3 ) ( 9 ) знак равно 54 π дюймы 2
≈ 169.64 дюймы 2
Общая формула для общая площадь поверхности цилиндра
Т
.
S
.
А
.
знак равно
2
π
р
час
+
2
π
р
2
.
Пример 2:
Найдите общую площадь поверхности цилиндра с радиусом основания 5 дюймов и высотой 7 дюймы.
Т
.
S
.
А
.знак равно
2
π
(
5
)
(
7
)
+
2
π
(
5
)
2
знак равно
120
π
дюймы
2
≈
376. 99
дюймы
2
99
дюймы
2
Площадь поверхности — формула, значение, примеры
Площадь поверхности трехмерного объекта — это общая площадь всех его граней. В реальной жизни мы используем концепцию поверхностей различных объектов, когда хотим что-то обернуть, нарисовать что-то и, в конечном итоге, при создании вещей, чтобы получить наилучший дизайн.Давайте узнаем все о площади поверхности трехмерных фигур в этой статье.
Что такое площадь поверхности?
Общая площадь, занимаемая поверхностями объекта, называется его площадью поверхности. В геометрии разные 3D-формы имеют разные площади поверхности, которые можно легко вычислить, используя формулы, которые мы изучим в этой статье. Площадь подразделяется на две категории:
.- Площадь изогнутой поверхности или Площадь боковой поверхности
- Общая площадь
Давайте узнаем об общих формулах площади поверхности различной формы.
Формулы площади поверхности
Для каждой геометрической формы существует своя формула площади поверхности, но основная идея состоит в том, чтобы получить общую площадь, занимаемую всеми гранями объектов. В этом разделе мы узнаем о различных формулах, используемых для расчета площади поверхности различных объектов. Общая площадь поверхности учитывает все грани трехмерной формы, включая плоские поверхности и изогнутые поверхности, в то время как площадь криволинейной поверхности вычисляется, чтобы найти площадь, занимаемую изогнутой поверхностью формы.Не включает площадь баз. Сфера — это одна трехмерная фигура, которая не имеет изогнутой поверхности, поскольку имеет только одну круглую поверхность без плоского основания.
Посмотрите на приведенную ниже таблицу, чтобы узнать формулы площади поверхности для различных трехмерных форм.
| 3D-форма | Общая площадь поверхности (TSA) | Площадь изогнутой поверхности (CSA) |
|---|---|---|
| Куб | 6a 2 | 4a 2 , где a — длина каждой стороны |
| Кубоид | 2 (фунт + верх + лев) | 2h (l + b), где l, b и h — длина, ширина и высота кубоида |
| Конус | πr (г + л) | πrl, где r — радиус, а l — наклонная высота конуса |
| Цилиндр | 2πr (в + г) | 2πrh, где r — радиус, а h — высота цилиндра |
| Сфера | 4πr 2 , где r — радиус сферы | Не применимо |
| Полусфера | 3πr 2 | 2πr 2 , где r — радиус полусферы |
Типы площадей
Как мы уже обсуждали, существует два типа площади поверхности для трехмерных форм: общая площадь и площадь криволинейной / боковой поверхности . Общая площадь поверхности включает в себя площадь всех граней формы, в то время как криволинейная или боковая область включает только площадь боковых граней фигур. Посмотрите на изображение ниже, чтобы понять разницу между общей площадью поверхности и площадью изогнутой поверхности. Для справки взята форма цилиндра.
Общая площадь поверхности включает в себя площадь всех граней формы, в то время как криволинейная или боковая область включает только площадь боковых граней фигур. Посмотрите на изображение ниже, чтобы понять разницу между общей площадью поверхности и площадью изогнутой поверхности. Для справки взята форма цилиндра.
Посетите эти статьи, чтобы узнать больше о площади поверхности различных форм.
Площадь призмы
Призма — это трехмерный твердый объект, состоящий из двух конгруэнтных оснований, которые представляют собой многоугольники и конгруэнтные боковые грани прямоугольной формы.Мы читаем о двух типах областей: во-первых, это площадь боковой поверхности призмы, а во-вторых, общая площадь поверхности призмы. Давайте узнаем подробнее. Боковая площадь призмы — это сумма площадей всех ее боковых граней, тогда как общая площадь поверхности призмы — это сумма ее боковой площади и площади ее оснований.
Площадь боковой поверхности призмы = периметр основания × высота
Общая площадь поверхности призмы = Площадь боковой поверхности призмы + площадь двух оснований = (2 × Площадь основания) + Площадь боковой поверхности = (2 × Площадь основания) + (Периметр основания × высота) .
Существует семь типов призм, основанных на форме оснований призм. Основания призм разных типов различны, как и формулы для определения площади поверхности призмы. См. Таблицу ниже, чтобы понять концепцию площади поверхности различных призм:
Часто задаваемые вопросы о Surface Area
Что такое определение площади поверхности?
Площадь поверхности — это общая площадь, покрытая всеми гранями трехмерного объекта.Например, количество краски, необходимое для покраски куба, и есть его площадь поверхности. Он всегда измеряется в квадратных единицах.
Какова формула площади поверхности?
Формула для нахождения площадей поверхностей различной геометрической формы заключается в сложении площадей каждой из их граней. Поиск площади каждой грани по отдельности может быть очень утомительным, поэтому у нас есть формулы площади поверхности для каждой геометрической фигуры. Некоторые формулы перечислены ниже:
- Общая площадь куба = 6 × (сторона) 2
- Площадь поверхности сферы = 4πr 2
- Общая площадь конуса = πr (r + l)
- Площадь криволинейной поверхности полусферы = 2πr 2
Площадь поверхности такая же, как и площадь?
Основное отличие состоит в том, что площадь поверхности — это площадь всех составных частей трехмерных фигур, таких как сфера, цилиндр и т.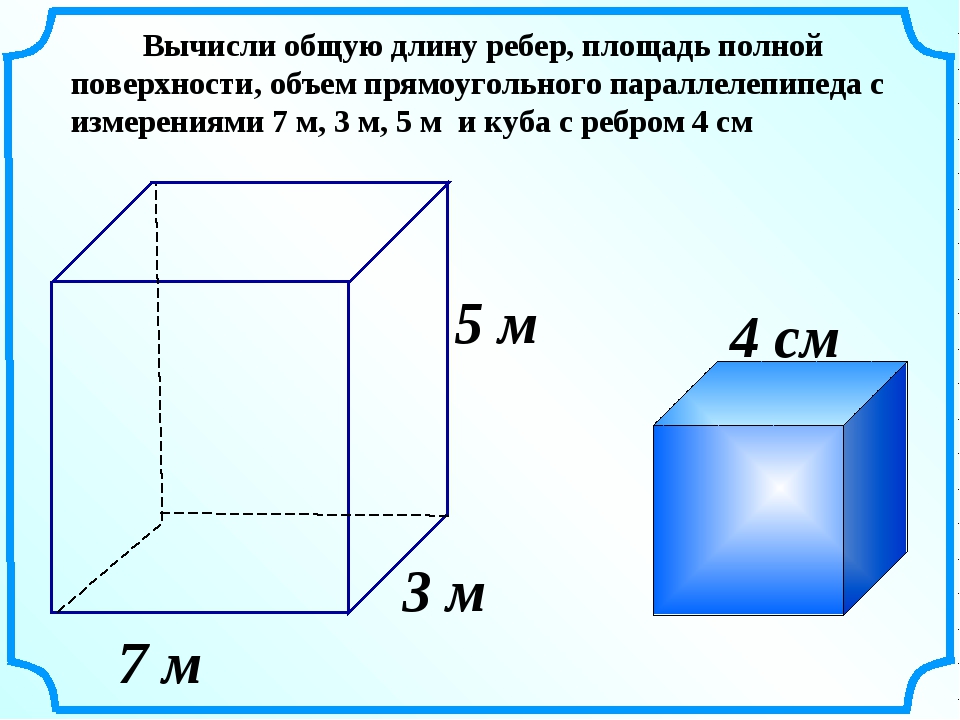 Д.тогда как площадь — это размер плоской поверхности, то есть двухмерной формы, такой как треугольник, квадрат и т. д.
Д.тогда как площадь — это размер плоской поверхности, то есть двухмерной формы, такой как треугольник, квадрат и т. д.
Как найти площадь поверхности прямоугольной призмы?
Мы можем найти площадь поверхности прямоугольной призмы, используя следующую формулу: S = 2 (фунт + bh + lh) квадратных единиц, где l, b и h — длина, ширина и высота прямоугольной призмы соответственно. .
Какова площадь поверхности куба?
Куб состоит из 6 квадратных граней.Итак, площадь поверхности куба — это сумма площадей всех этих 6 граней. Мы знаем, что площадь квадрата = a 2 , где a — длина стороны квадрата. Итак, площадь поверхности куба с длиной стороны a равна 6a 2 .
Какова площадь поверхности круга?
Площадь поверхности круга — это общая площадь, охватываемая границей круга, т. Е. Окружностью. Площадь круга с радиусом «r» задается как πr 2 .
Какова площадь поверхности конуса?
Измерение площади, занимаемой конусом, называется площадью поверхности конуса. Он задается как общая площадь поверхности конуса, T = πr (r + l), и площадь криволинейной поверхности конуса, S = πrl. Здесь «r» — радиус основания, а «l» — наклонная высота конуса.
Он задается как общая площадь поверхности конуса, T = πr (r + l), и площадь криволинейной поверхности конуса, S = πrl. Здесь «r» — радиус основания, а «l» — наклонная высота конуса.
Какова площадь поверхности цилиндра?
Площадь поверхности цилиндра — это общая область, покрытая поверхностью цилиндрической формы. Общая площадь поверхности цилиндра определяется как сумма площади боковой поверхности и площади двух оснований. Математически он выражается как 2πr (h + r) и выражается в квадратных единицах, например, m 2 , в 2 , cm 2 , yd 2 и т. Д.В то время как площадь криволинейной или боковой поверхности цилиндра составляет 2πrh квадратных единиц.
Площадь поверхности куба — формула, определение, примеры
Площадь поверхности куба можно определить как общую площадь, покрытую всеми шестью гранями куба. Общую площадь поверхности куба можно вычислить, если вычислить площадь двух оснований и площадь четырех вертикальных граней.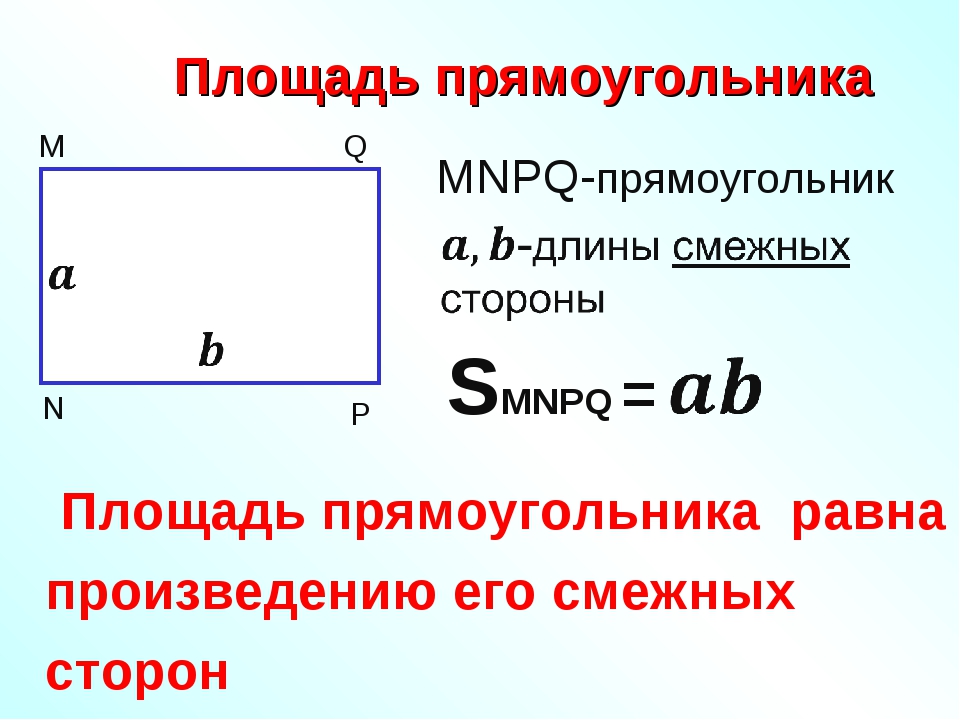 Куб — это трехмерная сплошная фигура, состоящая из квадратных граней. Площадь поверхности важно знать в ситуациях, когда мы хотим обернуть куб, покрасить поверхности куба и т. Д.
Куб — это трехмерная сплошная фигура, состоящая из квадратных граней. Площадь поверхности важно знать в ситуациях, когда мы хотим обернуть куб, покрасить поверхности куба и т. Д.
Какова площадь поверхности куба?
Площадь поверхности куба будет суммой площади оснований и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинаковых размеров, общая площадь поверхности куба будет равна площади одной грани, добавленной к самой себе пять раз. Оно измеряется как «количество квадратных единиц» (квадратных сантиметров, квадратных дюймов, квадратных футов и т. Д.). Площадь поверхности куба бывает двух типов,
- Площадь боковой поверхности
- Общая площадь
Общая площадь куба
Общая площадь поверхности куба — это общая площадь, покрытая всеми шестью гранями куба.Чтобы вычислить TSA, мы находим сумму площадей этих 6 граней.
Площадь боковой поверхности куба
Площадь боковой поверхности куба — это общая площадь, покрытая боковыми или боковыми гранями куба. Чтобы вычислить LSA, мы находим сумму площадей этих 4 граней.
Чтобы вычислить LSA, мы находим сумму площадей этих 4 граней.
Формула площади поверхности куба
Площадь поверхности куба может быть вычислена по длине ребра. Давайте поймем формулу для боковой и общей площади поверхности куба.
Общая площадь куба по формуле
Формула общей площади поверхности куба используется для определения площади, занимаемой шестью поверхностями. TSA куба получается путем умножения квадрата длины его стороны на 6. Таким образом, формула для площади поверхности куба со стороной «a» имеет вид «6a 2 ».
Общая площадь куба = (6 × сторона 2 ) квадратных единиц
Площадь боковой поверхности куба по формуле
Формула площади боковой поверхности куба используется для определения площади, занимаемой четырьмя боковыми или боковыми поверхностями.LSA куба получается путем умножения квадрата длины его стороны на 4. Таким образом, формула для площади боковой поверхности куба с длиной стороны «a» равна «4a 2 ».
Площадь боковой поверхности куба = (4 × сторона 2 ) квадратных единиц
Расчет площади поверхности куба
Общая площадь поверхности куба равна квадрату длины его стороны, умноженному на 6. Точно так же для площади боковой поверхности мы умножаем квадрат длины стороны на 4.Выполняя шаги, указанные ниже, мы можем найти площадь поверхности куба:
- Шаг 1 : Вычислите длину стороны куба.
- Шаг 2 : Найдите квадрат длины стороны куба.
- Шаг 3 : Для получения общей площади поверхности найдите произведение квадрата длины стороны на 6, а для площади боковой поверхности умножьте произведение квадрата длины стороны на 4.
- Шаг 4 : Напишите ответ в квадратных единицах.
Статьи по теме:
Проверьте эти интересные статьи, связанные с концепцией площади поверхности куба.
Часто задаваемые вопросы о площади поверхности куба
Что означает площадь поверхности куба?
Площадь поверхности куба определяется как общая площадь, покрытая поверхностями куба. Чтобы вычислить площадь поверхности куба, мы находим сумму площадей всех граней куба.
Какова площадь поверхности формулы куба?
Площадь поверхности куба с длиной ребра «а» может быть рассчитана по следующим формулам: LSA куба = 4a 2 квадратных единиц и TSA куба = 6a 2 квадратных единиц.
Какая единица используется для выражения площади поверхности куба?
Площадь поверхности куба выражается в квадратных единицах, например в таких единицах, как 2 , фут 2 , ярд 2 , м 2 , см 2 и т. Д.
Какова площадь боковой поверхности куба?
Боковая площадь куба — это общая площадь, покрытая боковыми или боковыми поверхностями куба. Формула для вычисления площади боковой поверхности куба имеет вид: Площадь боковой поверхности = 4a 2 , где «a» — длина ребра куба.
Формула для вычисления площади боковой поверхности куба имеет вид: Площадь боковой поверхности = 4a 2 , где «a» — длина ребра куба.
Какова общая площадь куба?
Общая площадь куба — это площадь, покрытая всеми шестью гранями куба. Формула для определения общей площади поверхности куба имеет следующий вид: Общая площадь поверхности = 6a 2 , где «a» — длина ребра куба.
Какова формула определения площади основания куба?
Формула для определения площади основания куба: 2 , где a — длина стороны куба.
Площадь поверхности кубоида
Общая площадь поверхности (TSA) кубоида — это сумма площадей его 6 граней, которая определяется по формуле:
TSA = 2 (lw + wh + hl)
Помните, что площадь поверхности — это общая площадь всех граней трехмерной формы.
Площадь боковой поверхности кубоида определяется как:
LSA = 2 (lh + wh) = 2 h (l + w)
Пример 1: Найдите общую площадь поверхности кубоида размером 8 см по формуле 6 см на 5 см.
TSA = 2 (lw + wh + hl)
TSA = 2 (8 * 6 + 6 * 5 + 5 * 8)
TSA = 2 (48 + 30 + 40)
TSA = 236
Итак, общая площадь поверхности этого кубоида составляет 236 см 2 .
Пример 2: Найдите площадь поверхности кубоида размером 4,8 см, 3,4 см и 7,2 см.
Решение:
Площадь грани 1: 4,8 × 7,2 = 34,56 см²
Площадь грани 2: 3,4 × 7,2 = 24,48 см²
Площадь грани 3: 4.8 × 3,4 = 16,32 см²
Сложение площади этих трех граней дает 75,36 см², поскольку каждая грань дублируется на противоположной стороне, общая площадь поверхности кубоида будет:
TSA = 2 (75,36) = 150,72 см²
Пример 3: Длина, ширина и высота прямоугольного прямоугольника составляют 10 см, 8 см и 7 см соответственно. Найдите площадь боковой поверхности кубоида.
Решение:
Площадь боковой поверхности кубоида определяется как:
LSA = 2h (l + w)
где,
l = длина = 10 см
w = ширина = 8 см
h = высота = 7 см
Вставьте эти значения в формулу, которую мы получим:
Пример 4: Длина, ширина и высота кубовида составляют 16 см, 14 см и 10 см соответственно. Найдите общую площадь поверхности кубоида.
Найдите общую площадь поверхности кубоида.
Решение:
Общая площадь поверхности кубоида определяется как:
TSA = 2 (l * b + b * h + h * l)
Подставляя значения в уравнение, мы получим
TSA = 2 (16 * 4 + 14 * 10 + 10 * 16)
TSA = 2 (224 + 140 + 160)
TSA = 2 * 524
TSA = 1048 см 2
Пример 5: Учитывая ящик для хлопьев длиной 20 см, высотой 30 см и шириной 8 см.Найдите площадь поверхности коробки.
Решение:
Чтобы найти поверхность коробки, нам нужно найти площадь каждой прямоугольной грани и сложить их все.
Площадь лицевой стороны: 20 х 30 = 600 см2.
Площадь верхней грани: 20 x 8 = 160 см2.
Площадь боковой грани: 8 x 30 = 240 см2.
Теперь сложите эти значения вместе, и мы получим: 600 + 160 + 240 = 1000 см2.
Таким образом, общая площадь поверхности составляет 1000 x 2 = 2000 см2.



 Через основание и высоту.
Через основание и высоту. 




 Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна:
Высота треугольника равна наклонной высоте пирамиды, s. Таким образом, площадь только одной из этих треугольных сторон равна: